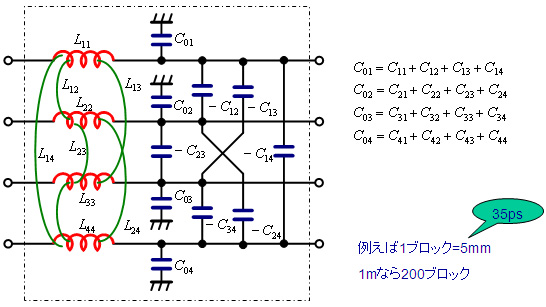
インテグリティな技術コラム(12，最終回) ―― 差動伝送のクロストーク・ノイズ

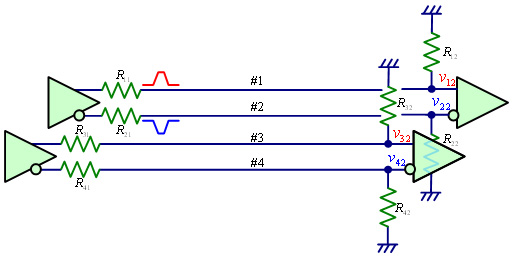
　一般信号のクロストーク・ノイズは，基本的には2本線路で解析し，複数の加害者（aggressorまたはd-ing）線路がある場合には，それらの重ね合わせで考えると分かりやすいと思います．差動伝送では，図1に示すように加害者線路が#1と#2の2本，被害者（victimまたはd-ed）線路が#3と#4の2本，それぞれ存在します．すなわち，少なくとも4本の結合線路を解析する必要があります．

図1　差動クロストーク

コラム・連載「インテグリティな技術コラム」 バック・ナンバ
第1回  反射波形にはさまざまな情報が詰まっている
第2回  パルス幅によって変化するノイズの影響
第3回  ラプラス変換による分布定数の解
第4回  ラプラス変換からフーリエ変換へ
第5回  差動インピーダンス
第6回  転換点は10年前，メモリが非同期型から同期型へ
第7回  スタブの反射はSSTLで回避
第8回  メモリ・バスの周波数特性と転送速度
第9回  メモリ・モジュールのクロック分配 
第10回  トーナメント方式のクロックにおける反射回避方法 
第11回  クロストーク・ノイズと二つの異なる伝送モード   

●差動信号と一般信号ではクロストーク・ノイズの及ぼす影響が異なる

　クロストーク・ノイズの及ぼす影響については，一般信号はクロックのタイミングにおけるノイズ・マージンを中心に考えます．極端な言い方をすれば，クロックから見たセットアップ時間とホールド時間の間のタイミング以外では，いくらノイズが乗っても構わないし，クロックのタイミングであってもノイズ・バジェットの範囲を超えないノイズであれば，許容できます．

　一方，差動信号の場合，ノイズの重畳によるタイミングの「ずれ」，すなわちジッタを重視することが多いので，信号の変化のタイミングにノイズが重なることを避けるために，ほとんど全てのタイミングを考慮しなければなりません．また，ノイズの絶対値についても，「この値以内なら誤動作しない」というノイズ・マージンの領域がなく，時間軸，振幅軸ともに一般信号よりも厳しく抑える必要があります．ただし，差動対に対して同相に乗ったノイズは，引き算によって低減されるという利点があります．

●4本線路では4×4のLCマトリックスになる

　一般信号の場合と同じように，ソルバを用いて，図2に示すようなプリント配線板の断面構造から線路パラメータを求めます．

図2　断面寸法とLCマトリックス

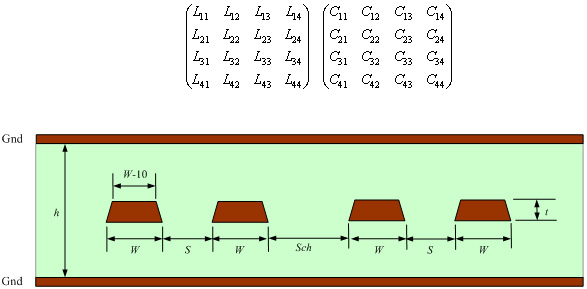
　2本線路の場合，2×2のLCマトリックスで波動方程式を解くと，2種類の伝搬速度とそれに対応した特性インピーダンスが得られました．それぞれのモードの特徴から，これらを，コモンとディファレンシャルと呼びました．

　4本線路の場合は，図2に示すように4×4のLCマトリックスとなり，4種類の伝搬速度と，これに対応した特性インピーダンスが得られます．各モードは，ある比率で伝搬します．これが，本コラムの第11回の最後に述べた図6の意味です．

●重ね合わせによる近似計算で概要をつかむ

　オーソドックスな方法では，4×4のマトリックスから導かれる波動方程式を解きますが，これはかなり煩雑なので，まずは別の簡単な方法を考えます．すなわち，加害者2本と被害者2本からそれぞれ1本ずつを選んで，2本線路とします．その組み合わせは，図3に示すように4通り存在します．

図3　差動クロストークの近似計算

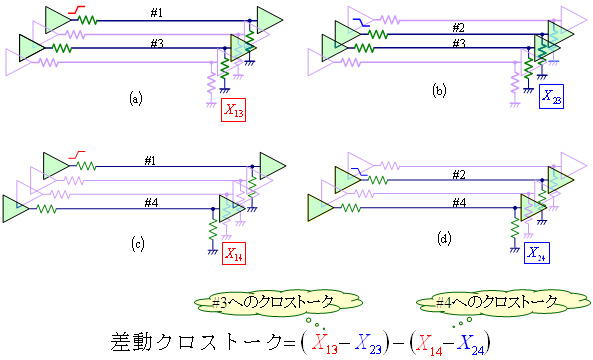
　図3(a)は，#1から#3へのクロストークです．図2の4×4のLCマトリックスから，図4に示すように必要な2×2のマトリックスを抜き出します．自己インダクタンスや自己キャパシタンスに相当する対角要素は，2本の線路のパラメータの平均とします．

図4　4×4マトリックスから2×2を抜き出す

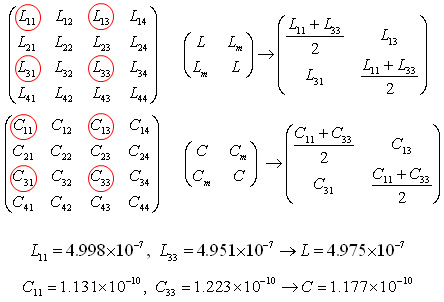
　2本線路のクロストークは，前回と同じ手法で求めることができます．すなわち，図5の2本の線路それぞれに1/2の信号を加えたときの遠端の電圧v_Cと，加害者に1/2，被害者に－1/2の信号を加えたときの遠端の電圧v_Dは，それぞれ以下のようになります．

図5　2本線路の遠端クロストーク

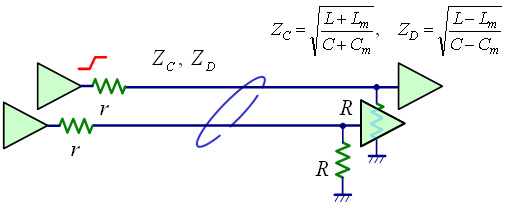
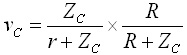.....(1)

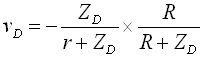.....(2)

　本コラムの第11回と同じように，式(1)と式(2)を加えると，被害者線路の遠端の電圧，すなわちクロストークvFが求まります．

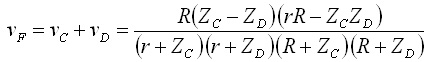.....(3)

　二つのモードの特性インピーダンスZ_CとZ_Dは，図5に示すようにL，L_m，C，C_mから求めます．

　図3のそれぞれの場合のクロストークの値を式(3)により求めて，図3(a)～(d)の4通りを式(4)で計算すると，差動クロストークの近似計算が行えます．

.....(4)

　式(4)において，X_mnのサフィックスのmは加害者の線路，nは被害者の線路を意味します．

　こんなことをしなくても，SPICEなどの回路解析ツールを使えばよいという考え方もあります．ただし，そのモデルは図6に示すようにかなり煩雑です．まず近似計算で概要をつかんでから，きちんと解析する必要のある場合にのみ解析するほうが手間が省けます．

図6　4本線路のモデル