FPGA活用回路＆サンプル記述集（1） ―― アナログ信号入出力回路

事例3．発振周波数を任意に設定できる数値制御型発振器

外部回路

• 回路図：図3-3
• 主要部品：R-2Rラダー（D-Aコンバータ）

HDL記述

• Verilog HDL記述：リスト3-1
• 外部入力：なし
• 外部出力：wave［7：0］（波形データ）
• 内部入力：di，clk，nreset
• 内部出力：なし
• パラメータ：なし

評価環境

• Altera社，Quartus II

　通常の論理回路では，システム・クロックの整数分の1の周波数しか生成できません．システム・クロックの整数分の1にならない周波数を発生させるには，PLL（Phase-locked Loop）を用いることができます．また，数値制御型発振器（NCO：Numerical Controlled Oscillator）という方法もあります．

　NCOではシステム・クロックをN分周した周波数のM倍を生成できます．例えば，システム・クロックを20.48576MHz（2²⁰×10Hz）として，これを2048576分周（20ビット）で分周すれば10Hz刻みの任意の周波数を生成できます．

　例えば米国Altera社のFPGAなら，MegaCoreのライブラリにNCOのファンクションがありますが，ほかのFPGAへ移行する場合に回路の変更が必要になります．このため，マクロ使用率や動作速度に余裕があれば，HDLで記述した方が自由度が上がります．

● NCOの動作原理

　図3-1がNCOのブロック図です．NCOはアキュムレータ（累加算器）そのものです．Nビットの累加算器にMを順次足し込んでいくことで求める周波数を得ます．ここで5ビットの累加算器を考えます．Mが1の場合，単純なカウンタそのものですから，クロックのたびに1ずつ値が増えて...
　　0→1→2→3→......→30→31→0→1
となります．Mが2なら一つとびで加算器の値は増えていきます．このようにMの値が大きいほど早く累加算器がロール・オーバして次の周期に入ります．従ってこの値でsinテーブル（正確にはcosテーブル）を引けば正弦波が得られます．図3-2は，Nを1?4とした場合です．

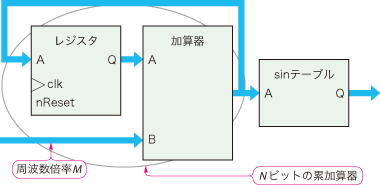
図3-1　数値制御型発振器のブロック図

図3-2　Nを1?4とした累積加算器の出力で得たsin波

　図3-3のように，このNCOからの出力をR-2Rの抵抗ラダーを用いてD-A変換することによって正弦波が得られます．もちろん，普通のD-Aコンバータを使っても構いません．その場合は使用するD-Aコンバータとのインターフェース回路を追加してください．また，通常のD-A変換と同じように，アンチエリアシング・フィルタが必要なのは当然ですが，それに加えて最低周波数の10分の1程度のカットオフ周波数のハイパス・フィルタを挿入します．

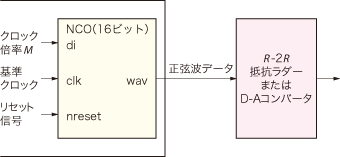
図3-3　NCO出力から正弦波を得る方法