インテグリティな技術コラム(10) ―― トーナメント方式のクロックにおける反射回避方法

●波形乱れを補正する

　式(6)の伝達関数は2τ₂ごとに1に漸近する時間応答となりますが，同式の分母に着目します．まず，分母をG(ω)とおきます．

..... (8)

　このG(ω)は，2τ₂だけ遅れた信号の振幅を1/2にして元の信号の3/2から減算することを意味します．元の波形にG(ω)の演算を施すと，分母子が約分されて，波形乱れのない時間応答が得られることが分かります．図7は，この補正を施した元の波形と遠端の波形を示します．

図7　補正入力波形と遠端波形

　この補正は，図5の2番目の線路の遅延時間τ2の2倍の遅れ時間と定数の掛け算と減算のみで実現できます．

　メモリ・モジュールへのクロック分配は通常8個となるので，4段のトーナメント方式となります．同じように計算すると，以下のようになります．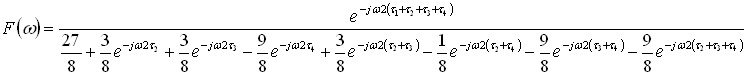

..... (9)

　級数展開すると極めて複雑な級数となりますが，分母だけに着目すると，いくつかの遅延と定数の掛け算および加減算で表されていることが分かります．すなわち，少し煩雑ではありますが，元の波形にこの演算を施すことにより，負荷端ではひずみのないきれいな波形が得られます．図8に，元の波形に演算を施した波形と負荷端の波形を示します．

図8　DIMMのトーナメント方式のクロックへの適用

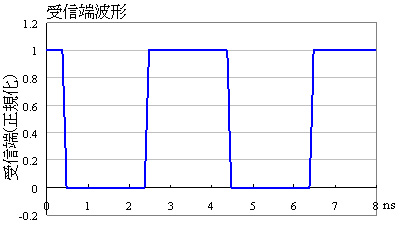
(a) T_w＝2ns



　　　　　　　　




 

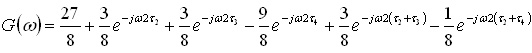
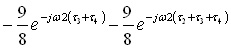
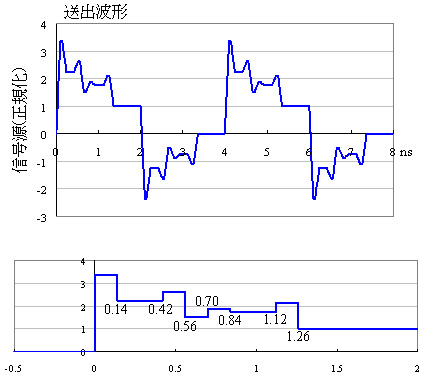
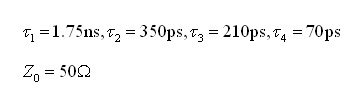
(b) T_w＝1ns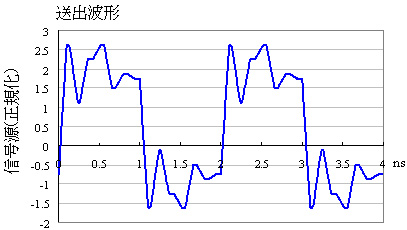

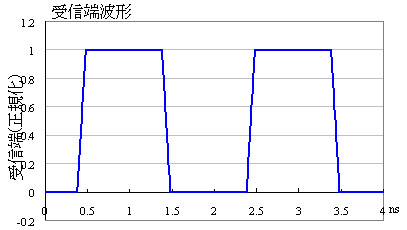
　図8(a)は広いパルス幅（2ns）の，図8(b)は狭いパルス幅（1ns）の場合です．この例では，補正の最大時間は2(τ₁＋τ₂＋τ₃)＝1.26nsなので，図8(a)ではパルス幅の間に補正が完了していますが，図8(b)では次の周期に繰り越しています．ただ，いずれの場合も波形ひずみは完全に補正されていることが分かります．