インテグリティな技術コラム(10) ―― トーナメント方式のクロックにおける反射回避方法

●縦続行列を用いて伝達関数を求める

　式(1)と，入力側および出力側の電圧と電流の関係により，伝達関数を求めることが出来ます．式がたくさん出てくるので，式の経過は稿末の付録にまとめます．図4のように，接続したときの伝達関数は付録の式(付4)のようになりますが，簡単化のため，遠端を開放（R₂＝∞）とすると，伝達関数は以下のようになります．

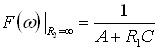..... (2)

図4　近端と遠端の条件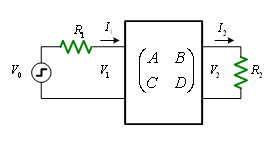

　線路の縦続行列は，以下のように線路の特性インピーダンスZ₀と遅延τを用いて表せます．

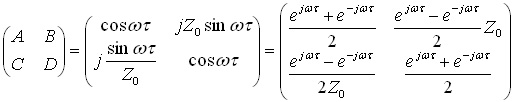..... (3)

　三角関数と指数関数はオイラー（Euler）の公式により互いに変換できますが，複数の線路の縦続接続の場合は，三角関数よりも指数関数のほうが便利です．

　図5に示す，トーナメント方式の最も簡単な2段の場合の縦続行列のA₁₂とC₁₂を求めると，式(4)および式(5)となります．

..... (4)

..... (5)

図5　最も簡単なトーナメント方式

(a) 最も簡単な2段のトーナメント方式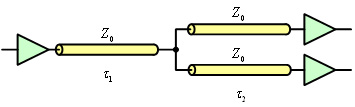


(b) 等価回路

　ここで，さらに簡単化のためにドライバの出力抵抗と線路の特性インピーダンスが等しい，すなわち送端終端を考えると，式(2)の伝達関数は以下のようになります．

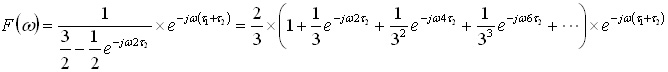..... (6)

　右辺に含まれる指数関数は，それぞれ時間遅れ，すなわちフーリエ逆変換において以下の関係であることを意味します．

..... (7)

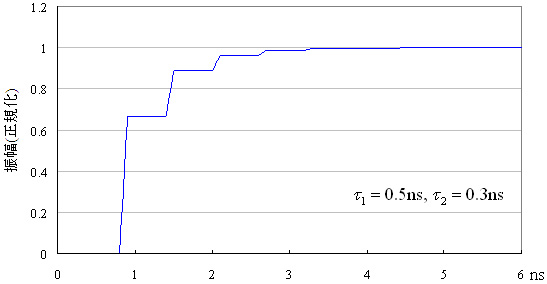
　式(6)の右辺の最後の指数はτ₁＋τ₂の時間遅れ，すなわち，図4のドライバからレシーバまでの総遅延時間です．かっこ内は，最初の振幅に対して2τ₂ずつ遅れるごとに1/3を掛けた振幅を加算することを意味し，その時間応答は図6のようになります．

図6　最も簡単なトーナメント方式の時間応答波形