インテグリティな技術コラム(8) ―― メモリ・バスの周波数特性と転送速度

●周波数帯域と転送速度の間の関係

　さて，図1のSDRAMを用いたメモリ4個のバスの周波数帯域は138MHzでしたが，NRZ（Non-Return-to-Zero） のパルスは，ほぼ2倍の276Mbps程度までは通りそうです．138MHzの正弦波を矩形波にすると，その2倍なので，「ほぼ」としたわけです．

　ここで，パルス波形のスペクトラムについて考えてみます．パルス波形の持つスペクトラムは，フーリエ変換を用いて求めることができます．図4(a)に示す，立ち上がり時間をゼロとしたときのパルス幅T_W，周期Tのパルスのフーリエ変換は，以下の式で求められます．

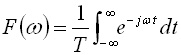..... (1)

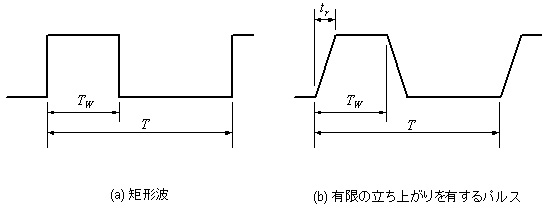
図4　パルス波形

　右辺は指数の定積分なので，計算は簡単です．

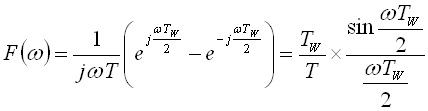..... (2)

　式(2)の右辺の係数T_W / Tは定数で，スペクトラムの形とは無関係です．図4(b)の有限の立ち上がり時間t_rを有する場合のスペクトラムは，係数を省略して，以下のように表されます．

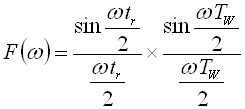..... (3)

　図5は，パルス幅T_Wと立ち上がり時間trの関係をt_r / T_W＝0.1～0.5としたときの式(3)を表したものです．

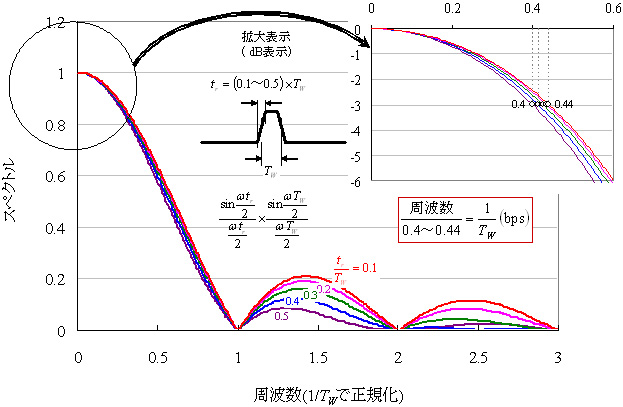
図5　スペクトラム

　横軸はパルス幅T_Wで正規化しています．図5の右上には，縦軸をデシベル（dB）で表して，帯域の定義の3dB下がった点を見つけると，ほぼ0.4付近になりました．すなわち，周波数（MHz）とNRZのパルスの転送速度（Mbps）の間には，「周波数＝0.4×転送速度」の関係があることが分かります．先に，転送速度は周波数のほぼ2倍と述べましたが，0.4の逆数の2.5倍となるわけです．

　従って，図2の周波数特性で110MHzの周波数帯域の場合，138×2.5＝346Mbpsの転送が可能と考えられます．モジュールの規格ではPC2700に相当します．図6は，このときのアイ・パターンを示しています．

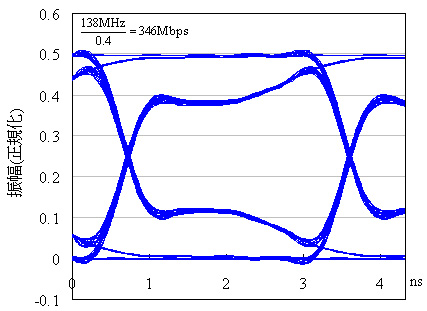
図6　負荷が4個のときのアイ・パターン