FPGAを使った数値演算回路実現の勘所(2) ―― 乗算器の構成を考える

●2進法の乗算を考える

　ここまでは10進法を基準に考えてきました．では2進法ではどうなるかといえば，何ら変わるところはありません．

　図2に2進法の110₂（6₁₀）×101₂（5₁₀）の例を示します．

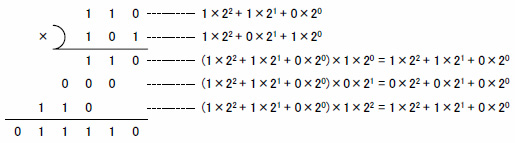
図2　2進法による乗算

　行っている操作は10進法の場合と同じですが，ただ1点だけ異なるところがあります．図2は図1(b)と同じように，被乗数はけた単位に分解せず，乗数のみけた単位に分解して処理しています．2進法で1けたに分解された乗数は係数が1，0のいずれかとなるので，aを被乗数，b_kを1けたに分解した乗数とすれば，以下のようになり，10進法において必要だった暗黙の加算が不要になります．

　　a×b_k＝aまたは0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(2)

　これは，部分積の演算結果が1ビットになり，けた上がりが生じないためです．従って演算の手順として，図1(a)と図1(b)の差がなくなるわけです．

　では，具体的な回路の実現方式はどうなるかを考えましょう．

　Step 1で必要な操作を考えてみましょう．まず，mビットの被乗数をa，nビットの乗数をbとすると，それぞれは式(3)，(4)のように表わせます．

　　a＝a_m-1×2^m-1＋a_m-2×2^m-2...＋a₁×2¹＋a₀×2⁰　　　　　　　　　　　　　　　　　　(3)

　　b＝b_n-1×2^n-1＋b_n-2×2^n-2＋...＋b₁×2¹＋b₀×2⁰　　　　　　　　　　　　　　　　　　(4)

　ここで1ビットの乗算は真理値表で表1のようになります．

表1　1ビット乗算の真理値表

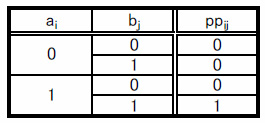
　乗算とはいってもAND（論理積）の機能と等価であることが分かります．従って，部分積ppを求める機能は式(5)のようになります．

　　pp_ij＝a_i & b_j　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(5)

　ここでiは被乗数aの任意のけた，jは乗数bの任意のけた，&はAND機能を表わす演算子とします．

　Step 2では求めたppをけたの重みに合わせて加算するわけですが，この様子を4ビットの場合を例にとって図3に示します．

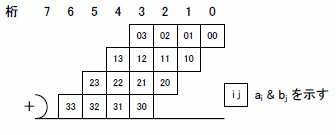
(a) 4ビット乗算の部分積

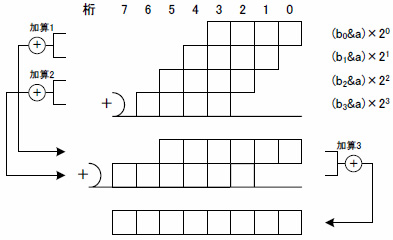
(b) 加算手順

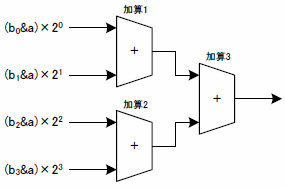
(c) 加算ブロック図
図3　Step 2の操作（4ビットの場合）

　図3(a)には部分積の配列を，図3(b)には加算の方法を，図3(c)にはブロック図化した回路構成を示しています．加算にはいくつかの方式があり，それぞれにメリットとデメリットがあるのですが，ここでは横1列に並んだビット列を多ビットの変数とみなし，順次加算する方式で説明しています．この場合，すべての加算器はキャリ（けた上げ信号）伝搬型の構造となります．

●符号付きの乗算を考える

　ここまでは，被乗数，乗数共に無符号として扱ってきました．では，符号付きの乗算を行いたい場合はどうしたらよいかを考えます．符号付き乗算の作法を知らないがために，乗算前に入力の絶対値をとり，乗算後に符号を戻すといった設計例を，過去に何度か見たことがあります．「それではいけないの？」と思ってしまった方，この際ですから正しい作法を身につけましょう．

　式(3)でaを符号付きの2の補数とした場合，負の値となるのはa_m-1のみであることを思い出してください．その他の係数a_m-2～a₀は全て正の数です．図4に，4ビットの符号付きの乗算における部分積の配列を示します．

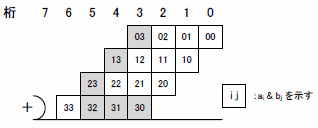
図4　4ビット符号付き乗算の部分積

　これら部分積の中で負の値となる（負あるいは0の値をとることになるが，0＝－0なのでこれも負であると考える）のは灰色に塗りつぶされた部分のみです．要するに変数の最上位と乗算を行っている項に限られ，最上位×最上位は負×負なので正となります．

　ここで，以下の変換式を思い出してください．

　　－a＝/a＋1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(6)

　/aはaの反転の意味です．部分積の加算を行う際，正の項と負の項が混ざっていると不便なので，式(6)を用いて部分積の負の項だけを正に変換してやります．これにより正負を意識せず，単純に加算できるようになります．この操作を図5に示します．

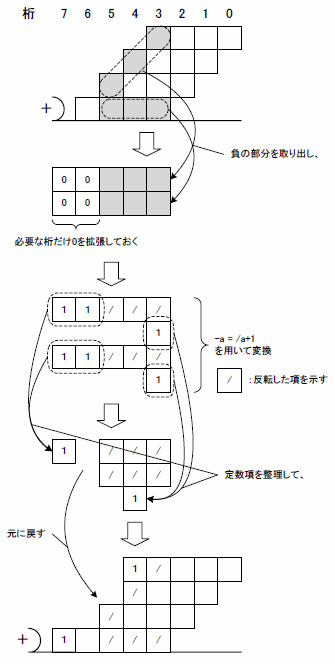
図5　部分積の負の項を正に変換

　ここまでくれば，あとは符号なしの場合と同じように加算を繰り返すだけとなります．どうですか？ 簡単でしょ？

●乗算器の中の加算方法について考える

　加算方法によるバリエーションについて説明しましょう．

　2項加算（多ビットの2変数加算で，加算器といわれる演算器はこの方式となる）は加算する項が1けた当たり2項しかありません．従って，下位からのキャリを待って演算を終了するキャリ伝搬型の構造となります．これに対して，乗算器における部分積を加算する際には，同一のけたに多くの項が存在します．下位からのキャリを待っている間に，演算できる項がたくさんあるわけです．

　フル・アダーの入力を考えてみれば分かりやすいでしょう．1ビット3項の入力に対して，2項加算では同一けたに2項しか加算項がないので，もう1入力は下位からのキャリとならざるをえません．一方，乗算器の部分積のような多項加算では，たくさんある項で3入力を満たすことができます．入力待ちの時間を減らすことができ，効率的と言えます．

　このような方式の代表がWallace Tree（ワラス・ツリー）というフル・アダーをアレー状に連結して加算を繰り返す方式です．同一けたにある多数の項をキャリ待ちすることなく演算し，最終的に2項になるまで演算します．2項になったところで2項加算を実行して演算終了となります．4ビット加算の適用例を図6に示します．

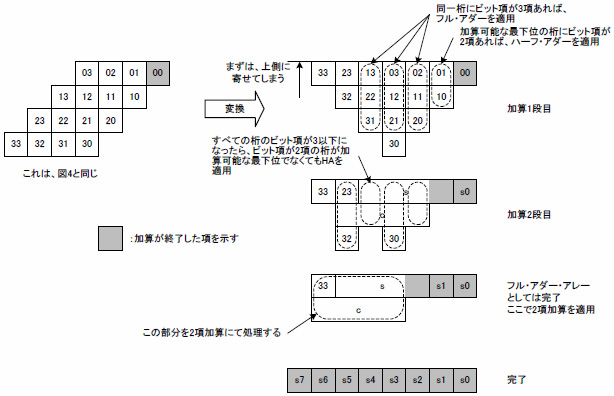
図6　Wallace Treeによる加算手順