FPGAを使った数値演算回路実現の勘所(1) ―― 加算器の構成を考える

鈴木昌治

技術解説 2010年7月 1日

本連載では，数値演算回路をFPGA上に展開する際の考え方や注意点について紹介します．回路構成の自由度の高いASICとは異なり，FPGAでは用意されているデバイス・アーキテクチャ（論理ブロックやメモリ・ブロック，配線の構造）に逆らわないように回路を作り込む必要があります．第1回では，FPGAに実装する加算器の回路構成について解説します．（編集部）

　FPGA（Field Programmable Gate Array）が市場に登場したのは1985年，米国Xilinx社の「XC2000」が最初なのだそうです．今年で四半世紀の節目を迎えるわけです．初期のころのデバイスはASIC（Application Specific Integrated Circuit）などのプロトタイピングに利用されたと聞きますが，筆者はもっぱら少量生産品に利用していました．

　当時のものはゲート規模が大きくないわりに高価でした．安価な製品の開発には決して使用できないものでしたし，配線をSRAMスイッチで切り替えるタイプは，ASICと比べものにならないくらい動作速度の遅いデバイスでした．そのため，例えば画像系の信号処理などにはまったく使えなかったと記憶しています．開発ツールも，当時はWindowsなどありませんから，DOS画面上で動作する質素なものでした．配置配線に恐ろしく時間がかかり，ちょっと大きなデザインで配置配線を行うと，数日かかっても終わらず，最後に配線できなかった旨のメッセージが出てきて終了，なんてことも珍しくありませんでした．確か配線を手動で行うツールも付いていて，その作業に苦労された方も多いのではないでしょうか．筆者も当時は，FPGAに対してあまり良い印象を持っていませんでした．

　さて今はと言うと，まさに隔世の感があります．ゲート単価は下がり，動作速度も上がっています．ハイビジョン画像を4倍速クロックで処理することも可能になりました．ASICでなければできなかった範囲が急激に狭まり，その上，開発のリスクが低いのですから，少量生産品のアプリケーションでは，まずFPGAが採用されるケースがほとんどではないでしょうか．量産品についても，FPGAで作ったプロトタイプの設計をそのままコピーして量産する手段が確立しています．FPGA全盛の時代を迎えたといえます．

●FPGAの構造に適した数値演算回路の構成を検討する

　「適材適所」という言葉があります．ディジタル回路の実現手段として何を（どのデバイスを）選ぶかにより，回路方式を決める必要があることは言うまでもありません．ディジタル数値演算回路は，CPU（Central Processing Unit）に代表されるカスタムICでいかに性能を引き上げるかを主眼に回路方式が研究されてきました．一方FPGAの内部構造は，種々の回路実現に対してまんべんなく（そこそこの）性能を発揮するように作られており，数値演算回路専用の構造にはなっていません．つまり，従来，考えられてきた回路方式が必ずしもFPGAの構造に適しているとは限りません．

　ここではFPGAにおける数値演算回路の実現方法について，今一度，考えてみましょう．今回は，加算器（アダー）について考えていきます．

1．加算器の構成法をおさらい

　加算器の基本回路はリプル・キャリ・アダー（Ripple Carry Adder）です．これは，小学生の時に習った筆算による足し算をそのまま2進数に置き換えて実現した回路です．

●リプル・キャリ・アダーは筆算と同じように計算

　1けた当たりの計算内容は，以下のとおりです．

　　　　　　　　　　　　　　　　　　　　　　　　　(1)

　a_n，b_nは各けたの入力変数，c_n-1は下位からのキャリ（Carry；繰り上がり，あるいはけた上がり），s_nは自けたの和，c_nは上位けたへのキャリ（1けた上になるので，×2してある）になります．式(1)の機能は，「右辺の1ビットの3変数を加算して，自けたの和と上位けたへのキャリとする」と考えることができます．この機能をフル・アダー（Full Adder）と言います．

　加算器においては，下位けたから上がってきたキャリを上位けたに伝えるキャリ・チェーンが遅延性能を決定します．式(1)において，a_n，b_n，s_nは自けた内で完結している演算であるのに対し，c_n-1，c_nの部分はけた間を伝搬し，最終的には最下位から最上位まで連結することになるからです．キャリ・チェーンの1けた分の機能は表1の真理値表のようになります．

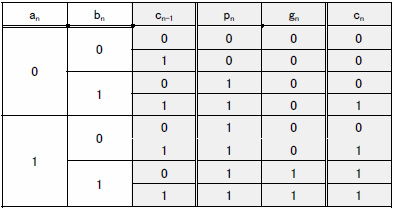
表1　キャリ・チェーンの真理値表（灰色の部分がキャリ・チェーンに直接関与する論理）

　ゆっくり考えれば誰でも理解できる論理です．これを式に表わすと式(2)に，回路図で表現すると図1のAND-OR（論理積-論理和）回路になります．

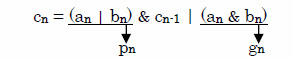　　　　　　　　　　　　　　　　　　　　(2)

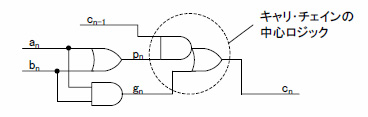
図1　キャリ・チェーン

　p_nはプロパゲーション（Propagation）で下位からのキャリを上位に伝達する役目，g_nはジェネレーション（Generation）でここでは自けたから生成されたキャリを示す変数です．いずれも加算器を説明する上で重要な機能を持っています．

●自由度の高いASICではネットワーク・アダーが主流

　リプル・キャリ・アダーでは，最下位から最上位まで延々と続くキャリ・チェーンの遅延時間を短縮すれば，加算器全体の信号遅延を改善できます．この方法として考えられたのがキャリ・ルックアヘッド・アダー（Carry Look Ahead Adder；けた上げ先見加算器などと訳される）です．

※ 加算回路の方式の詳細については，拙著「ディジタル数値演算回路の実用設計」（CQ出版社刊）に記述があるので，詳細はそちらを確認してください．

　ところが，キャリ・ルックアヘッド・アダーには欠点がありました．加算のけた幅が大きい場合に原理に忠実に設計してしまうと，多入力AND-ORが必要となり，ファンアウト数も大きくなるという問題です．キャリ・ルックアヘッド・アダーは，回路を構成するゲートのトランジスタ・サイズが大きい時代はある程度意義のある回路でしたが，現代のように半導体の製造プロセスが微細化され，トランジスタが小さく，配線が細くなってくると，現実的ではなくなってきます．

　そこで考えられたのがキャリ・ルックアヘッド・アダーの改善版ともいえるネットワーク・アダー（Network Adder）です．これは演算上の中間項をバランスよく再利用し，ファンアウトを分散させて一定以上の数にならないようにした方式です．ASICなど，実現手段の自由度が高い場合にはこの方式が主流となっています．

　駆け足ではありますが，加算回路の基本構成についておさらいしました．加算器にはこのほかにもさまざまな方式があります．

tag: EDA, FPGA, LSI, 開発手法