FPGAを使った数値演算回路実現の勘所(1) ―― 加算器の構成を考える

2．FPGAベンダによる加算器構築の努力

　では，実際にFPGAで加算器を実現するに当たって，どのような回路が好ましいのかを考えてみることにしましょう．そのためには，まずFPGAベンダがどのような構造をFPGAの上に作り込んでいるのかを知る必要があります．Xilinx社と米国Altera社のFPGAを例として取り上げます．

●Spartan-3のスライスを見る

　筆者が手慣れているという理由で，まずはXilinx社のSpartan-3ファミリを題材とすることにします．後継としてSpartan-6ファミリがありますが，Spartan-3はまだまだ現役のデバイスです．

　Spartan-3で加算器を実現する基本構成はリプル・キャリ・アダーです．ただし，単純なフル・アダーの連結によって実現しているのではなく，キャリ・チェーンを抜き出して専用ハードウェア化することにより，加算器としての高速性を実現しています．これをXilinx社は「ルックアヘッド・キャリ加算」と呼んでいます．

　ルックアヘッド・キャリ加算はフル・アダーを2段のハーフ・アダー（Half Adder；式(1)からc_n-i入力を省いた機能となる）に分離し，「下位からのキャリを待っている間に入力変数の同一けたの加算だけはやってしまおう」という考え方の回路で，いわゆるキャリ・ルックアヘッド・アダーとは趣を異にします（基本的な意味では同じだが...）．なお，これはXilinx社特有の回路方式ということではなく，ごく一般的な回路です．

　図2にSpartan-3ファミリのスライスの構成を示します．加算機能に注目したうえで，簡略化してあります．下側のCINから上側のCOUTに抜けるまでがキャリ・チェーンで，2ビットで構成されています．これを縦に連結することで，大きなビット幅のキャリ・チェーンを構成します．このラインが高速でないと，基本的に高速な加算器が作れません．そこでできる限り余計なゲートを省き，1ビット当たりマルチプレクサ1個で構成されています．もちろんAND-OR回路が1個あれば済む話なのですが，汎用性を考えてマルチプレクサを置いているようです．

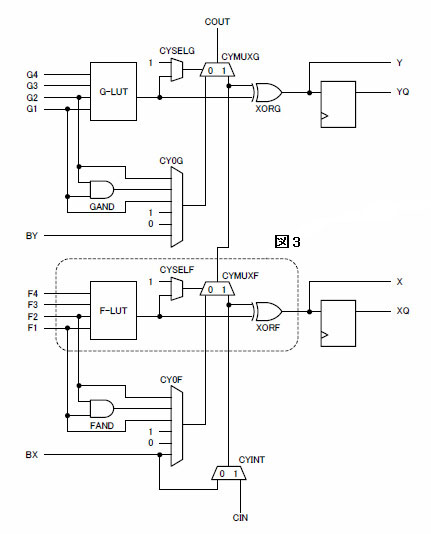
図2　キャリ・チェーン周辺のスライス構成（簡略図）

　ここを中心に，1ビット当たりのアダーをどのように構成するかを図3に示しました．

　基本的には式(1)が実現できればよいのですが，図3(a)の回路はXilinx社がユーザーガイドで説明している方式，図3(b)の回路はより式(1)の原理に近い方式です．いずれも2分割されたフル・アダーの初段のハーフ・アダーのEXOR（排他的論理和）をLUT（Look-up Table）上で実現しており（Propagation＝Half_sum），ANDを実現する部分（Generation）に差が見られます．

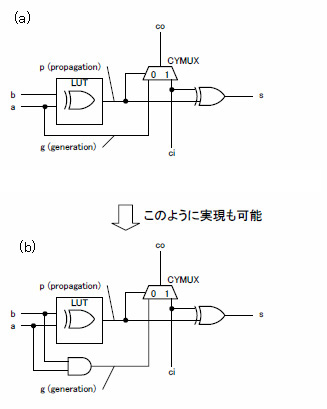
図3 　1ビット当たりのアダーの実装

　図3(b)の回路では，乗算器をロジック・セルで実現する場合の部分積生成用のANDを流用しています．下位からのキャリとの和を求める後半のハーフ・アダーについてはサム用EXORを専用ゲートにて，キャリ用AND-OR回路は先ほど述べたマルチプレクサ（CYMUX）にて実現しています．

　どちらも実装可能で，論理的には等価です．同じ論理に見えない方は表2で確認してみてください．そもそも後半のAND-ORでキャリ・チェーンを構成することが前提の場合，前半のハーフ・アダーは冗長な論理です．Xilinx社のお勧め回路は，そこをうまく使っているといえます．

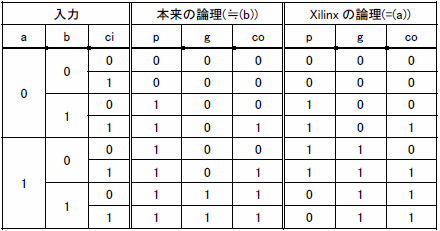
表2　Xilinx社のFPGAによるキャリ生成論理の違い

　同社のVirtex-5やVirtex-6，Spartan-6などでも，若干の差異は見られるものの，基本的な実現方法は同じです．「キャリ・チェーンの最適化」，「専用線，専用ゲートの利用」，「余分なゲートの非通過」を徹底的に行っているため，ファミリが新しくなっても，これ以上進化のしようがないのでしょう．若干の差異とは，1スライス当たりのビット数を4ビットとし，CYINTの出現頻度をさらに下げている点などです．