CUDA技術を利用したGPUコンピューティングの実際（後編） ―― FFTを利用した光波の伝播（フレネル回折）をGPUで高速計算

　これらの値を入力すると，図6の（3）の部分にマルチプロセッサ当たりのブロック数や，ブロック当たりのワープ数などが計算されます．また，（4）にグラフとして表示されます．図6によると，Kernel2は，マルチプロセッサ当たり2個のブロックと16個のワープが割り当てられていることが分かります．

　計算速度はカーネルの実装方法に依存するため，ここで示された数値が高いからといって計算速度が向上するとは限りません．一つの目安としてとらえてください．

3．FFTを応用した計算の高速化

　次に，数値計算や画像処理でよく使われる高速フーリエ変換（FFT：Fast Fourier Transform）を応用した計算の高速化事例を紹介したいと思います．ここでは，光の伝播計算によく使われるフレネル回折を例として取り上げます．

　フレネル回折は光学の幅広い分野で使われる計算方法で，さまざまな応用例があります．例えば，ホログラフィ技術を応用した顕微鏡で撮影したホログラムから光の伝播を計算し，微小物体の3次元像をコンピュータ内に再生する場合や，回折光学素子や微小な機械部品の集合体であるマイクロマシンなどに光を照射したとき，その透過光（もしくは反射光）分布を計算したい場合などに使われています．

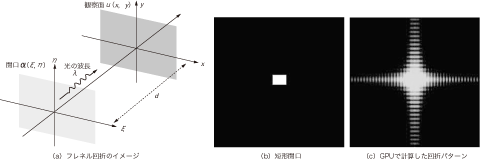
図8　フレネル回折
（b）では，白い部分については穴が開いており，光が通過する．黒の部分は光を遮断する．（c）では，フレネル回折の計算結果をコントラスト調整し，256階調の画像として表示している．

　フレネル回折のイメージは図8（a）のようなものです．何らかの物体（光学では開口と呼ぶ）を開口面α（ξ，η）に置き，左から波長λの光を入射したときに，その開口によって入射光が回折されます．その回折光が距離dだけ伝播したとき，観察面u（x，y）の光の分布の様子を計算するものがフレネル回折積分です．

　光は振幅と位相を持つ波なので，複素数で表現すると便利です．また，開口は入射光の振幅と位相の両方を変調するため（振幅か位相のどちらかだけを変調する開口もある．ここで扱う開口は振幅のみを変調する），開口も複素数として取り扱うと便利です．観察面の光の分布も複素数となります．

　ここで簡単な例として，開口面に図8（b）の矩形（くけい）開口を置き，左側からレーザを照射したときの観察面の回折パターンを見てみます．

　この例は物理学の教科書で光の波動性を説明する際によく取り上げられますが，観察面では図8（c）のような回折パターンを得ることができます．この回折パターンは，実際に以下で説明する方法でCUDAを用いてGPUで計算させたもので，実際の実験結果とよく似た計算結果を得ることができています．