音声信号処理の基礎理論（前編） ―― 音声圧縮，ノイズ除去，音源分離で用いられる理論

● 独立と無相関の違い

　例えば，図16(a)に示すような，平均が0の二つの確率信号x₁とx₂を考えます．

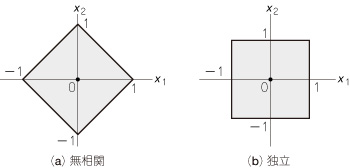
図16　無相関と独立の違い
平均が0の二つの確率信号x₁とx₂を示す．結合確率密度関数p（x₁，x₂）は，（x₁，x₂）に対する出現確率の大きさを誌面と垂直方向にとり，3次元描画する必要がある．ここでは，四角形内部の各点に対する出現確率は一定，四角形外部はすべて0とする．

　結合確率密度関数p（x₁，x₂）は，（x₁，x₂）に対する出現確率の大きさを誌面と垂直方向にとり，3次元描画する必要がありますが，ここでは，四角形内部の各点に対する出現確率は一定，四角形外部はすべて0とします．

　図16(a)では，重みが一定なので，期待値は実現可能な値をすべて足したものの定数倍に等しくなります．実現可能な値がそれぞれ正と負に同じ絶対値を持つので，

　　 .....(16)

となり，x₁とx₂は無相関であることが分かります．

　しかし図16(a)を見ると，x₁とx₂のいずれか一方が正か負の大きな値をとる場合，他方は小さな値しかとらないことが分かります．つまり，一方の実現値が他方の実現値に影響を与えているので，直感的にも二つの確率信号は独立ではありません．

　これに対して，図16(b)では，二つの確率信号x₁とx₂の実現値は互いに影響を与えていません．このとき二つの確率信号は独立です．

　従って，図16(a)の例では，p（x₁，x₂）の分布を0を中心に回転すると，すべて無相関となりますが，独立となるのは，回転の角度がnπ/2（nは整数）のときだけであることが分かります．

　このように，無相関と独立の扱いには注意が必要です．

● 定常と非定常

　ノイズ除去では，最初の数フレームの平均スペクトルをノイズの推定値とします（図17）．これはノイズの統計的性質が時間によらず一定であることを期待した処理となっています．

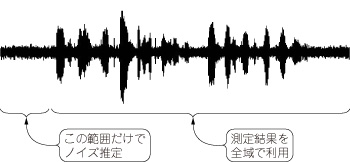
図17　ノイズが定常の場合
ノイズが定常だったら，時間によらず同じノイズ推定値を使ってよい．

　このように，ある確率信号の統計的性質が時刻nとともに変化しない場合，その確率信号は，定常であるといわれます．

　定常は，さらに二つの状態に分類されます．もし，

　　 .....(17)

　　 .....(18)

のように，平均値が時間によらず一定で，式(18)が時間差kのみの関数となるとき，確率信号は弱定常と呼ばれます．例えば，ガウス分布は平均値と分散でその分布形状が完全に決定するので，弱定常ならば統計的性質は時間によって変化しません．ガウス分布を扱う場合，"定常"は弱定常を意味することが多くなります．

　一方，高次の結合確率密度関数が，

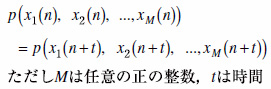　　 .....(19)

のように時間によって変化しない場合は，強定常と呼ばれます．強定常は，2次の統計量までしか考慮しない弱定常よりも強い制約です．ICAなどでは高次の統計量を扱うことが多いので，この場合の"定常"は，強定常を意味することが多くなります．

　また，確率信号の統計的性質が時間的に変化する場合には，非定常と呼ばれます．

● 中心極限定理

　互いに独立で，同一の確率分布に従う複数の確率信号を「i.i.d.な確率信号」と呼びます．

　i.i.d.な確率信号x₁，x₂，...に対し，図18の中心極限定理が知られています⁽¹⁾．

図18　中心極限定理

　この定理を大雑把に述べると，確率信号の和が従う確率密度関数は，元の確率密度関数よりもガウス分布に近づいているということです．第4章で説明したICAによるブラインド音源分離では，この原理を利用し，分離信号の確率密度関数がガウス分布から遠ざかるように分離行列を更新しています（図19）．

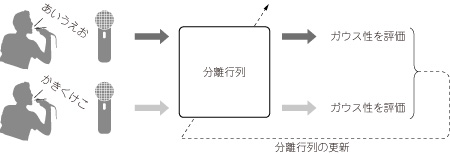
図19　中心極限定理の音源分離への応用
ICAによるブラインド音源分離では，この原理を利用し，分離信号の確率密度関数がガウス分布から遠ざかるように分離行列を更新している．

（後編へ続く）

参考・引用*文献
(1) 村田昇；入門 独立成分分析，東京電機大学出版局，2004年．
(2) 飯國洋二；基礎から学ぶ信号処理，培風館，2004年．
(3) 古井貞熙；ディジタル音声処理，東海大学出版社，1985年．
(4) サイモン ヘイキン（著），武部幹（訳）；適応フィルタ入門，現代工学社，1987年．

かわむら・あらた
大阪大学大学院 基礎工学研究科 システム創成専攻 助教
おち・ひろし
九州工業大学大学院 情報工学研究院 電子情報工学研究系 教授