音声信号処理の基礎理論（前編） ―― 音声圧縮，ノイズ除去，音源分離で用いられる理論

● Scilab演習 ―― ガウス分布のヒストグラム

　残響が消えにくいトンネル内では，壁面からの多数の反射音の和としてノイズが観測されます．このような多数の確率信号の和の分布はガウス関数に近づくことが知られています⁽¹⁾．そこでトンネル内で収録したノイズのヒストグラムを作成し，ガウス関数と比較してみましょう．

　Scilabのプログラムをリスト1に，結果を図9に示します．結果から，両者がほぼ一致しており，現実の確率信号の和の分布もガウス分布に近づくことが分かりました（Scilabで使用するプログラムやデータは，こちらのWebページからダウンロードできる）．

リスト1　ガウス分布のヒストグラムを作るプログラム（3-1-1_tunnel_hist.sce）

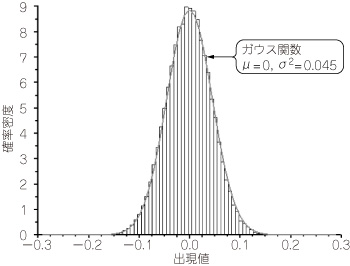
図9　Scilabで作成したガウス分布のヒストグラム
トンネル内で収録したノイズのヒストグラムである．

● 確率分布関数

　確率信号xのある範囲A～Bの出現確率が知りたいとき，その確率密度関数であるp（x）を用いて，

　　 .....(1)

を計算します．しかし，範囲A～Bを設定するたびにこのような積分計算を行うことは面倒です．そこで，

　　 .....(2)

であることを利用し，

　　 .....(3)

を多くのAに対して求めておきます．そして図10のように，任意の範囲A～Bに対して，

　　 .....(4)

を計算すれば出現確率を知ることができます．

図10　確率分布関数による出現確率の計算
範囲A～Bの出現確率は二つの確率分布関数から計算できる．

　式（3）は確率分布関数と呼ばれます．

　図11にガウス分布の確率密度関数と確率分布関数の性質を示します．確率密度関数と確率分布関数は，一方が与えられれば，他方が導出できるので，一般的には「～分布に従う」確率信号という言い方をします．この場合の「～分布」は，確率密度関数と確率分布関数の両者を区別せずに表現していることに注意が必要です．

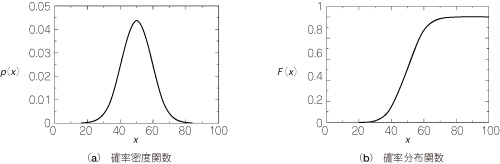
図11　確率分布関数とその性質
確率密度関数と確率分布関数は，一方が与えられれば，他方が導出できる．

● 結合確率密度関数

　複数の確率信号が同時に生じる場合の確率密度関数について考えます．

　複数の確率信号x₁，x₂，...，x_Mが同時に生じる場合の確率密度関数をp（x₁，x₂，...，x_M）と表すとき，これを結合確率密度関数と呼びます．同時にM個の確率信号が生じるときは，いずれかの実現値がほかの実現値に影響を与える場合があります．このため通常は，個々の確率密度関数p（x₁），...，p（x_M）が既知であってもp（x₁，...，x_M）を得ることは困難です．

● 期待値

　実現値以外に確率信号を記述する方法として，次の期待値が有用です．

　期待値について理解を深めるため，図12(b)のような数が詰まった袋xを考えます．この例では，1，2，5の3種類の数字がそれぞれある割合で袋の中にたくさん入っていると考えます．袋から数字を取り出して，袋にまた戻すという作業を繰り返します．このとき，作業の前後で袋の中の状態は変わらないとします．

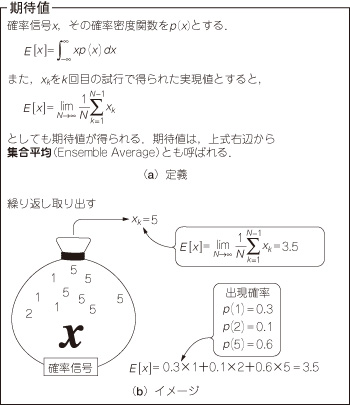
図12　期待値
無限回の試行の平均をとることで期待値が得られる．

　k回目の試行で袋から取り出した数字を実現値x_kと書くと，図12(a)の下の式の右辺のように，無限回の試行の平均をとることでxの期待値が得られます．また，袋の中の数の割合，すなわち出現確率p（x）が分かっているときには，図12(a)の上の式のように，xがとり得るそれぞれの値にp（x）を重みとして与え，期待値を得ることもできます．

　いずれかの方法によって得られた値〔図12(b)の例では3.5〕は，実現値の平均の大きさを表しています．従って，E［x］を特にxの平均と呼びます．

　また，確率信号の平均値からの散らばりの程度を示すものとして分散があります（図13）．

図13　分散
確率信号の平均値からの散らばりの程度を示す．

　平均と分散は信号処理の分野で特に頻出する期待値です．