音声信号処理の基礎理論（前編） ―― 音声圧縮，ノイズ除去，音源分離で用いられる理論

● ヒストグラム

　確率信号では，未来の値を特定することはできませんが，どのような傾向で実現値が生じるかを知りたいという要求はよくあります．そのためには，確率信号の実現値の出現の傾向を「見る」ことが有用になります．

　そこでまず，確率信号xのk回目の試行における実現値x_kを，

• 0≦x_k＜1ならグループ1
• 1≦x_k＜2ならグループ2

のように，ある範囲ごとにグループ分けします．もちろん，値そのものをグループと設定しても構いません．このグループをクラスと呼びます．

　次に，それぞれのクラスに含まれる実現値の個数を数えます．この数は度数と呼ばれます．

　横軸をクラス，縦軸を度数としてプロットします．こうすることで，各クラスに含まれる実現値の出現傾向を「見る」ことができます．この横軸をクラス，縦軸を度数で表したものをヒストグラムと呼びます．

　ヒストグラムを用いると，その確率信号の出現しやすい値と，出現しにくい値を見極めることができ，確率信号の性質を知る上で非常に有用です．

　例として，音声のヒストグラムを図5に示します．クラスは，最小値から最大値までを100等分したそれぞれの範囲としています．音声では発声が停止する時間が多く含まれるため，クラス0付近（振幅が0に近い）の振幅値の出現回数が非常に多いことが分かります．

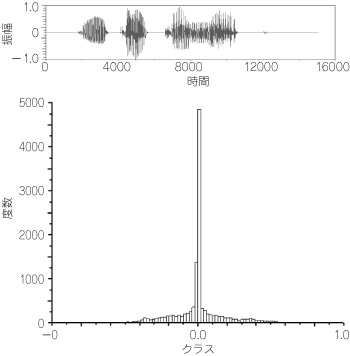
図5　音声信号のヒストグラム
横軸をクラス，縦軸を度数で表したものがヒストグラムである．図は音声のヒストグラムである．音声では発声が停止する時間が多く含まれるため，クラス0付近の振幅値の出現回数が非常に多いことが一目で分かる．

● 確率密度関数

　確率信号のそれぞれの値が，どれくらい出現しやすいかが分かっているとき，「確率分布が与えられている」と表現します．

　確率分布を表す関数として，確率信号の各値の出現確率を負の方向から積分して積み上げた確率分布関数と，微小区間の値の出現確率を表した確率密度関数があります．

　確率信号をx，その確率密度関数をp（x）とすると，p（x）には図6のような性質があります．

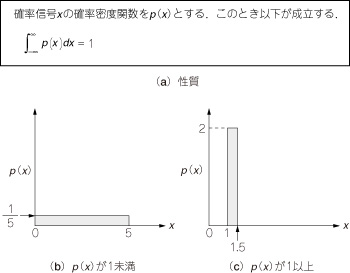
図6　確率密度関数（PDF）の性質
確率信号xのいずれかの実現値が必ず生じることを保証する．

　図6中の式は，確率信号xのいずれかの実現値が必ず生じることを保証しています．また，ヒストグラムを正規化した場合，図6(a)の式と同じ性質を持つので，確率密度関数の近似曲線が得られます．

　ここで，ある範囲の値の発生確率が等しく，そのほかの値は生じないような確率信号xを考えます．
p（x）は図6の式を満たすxの確率密度関数とします．

　図6(b)の確率密度関数では，p（x）の値が常に1未満ですから，直感的に出現確率をイメージしやすいでしょう．しかし，xの値と分布の形によっては，図6(c)のようにp（x）が1より大きくなる場合があることに注意が必要です．

　代表的な確率密度関数には，ガウス分布があります（図7）．そのほかの確率密度関数としては，一様分布，指数分布，レイリー分布，ガンマ分布などがあります．

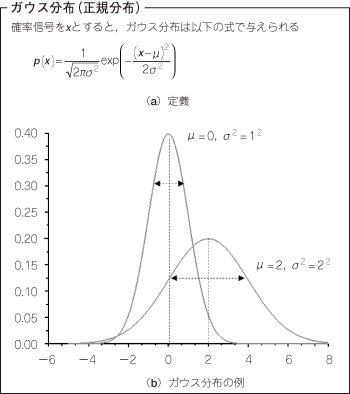
図7　ガウス分布の例
代表的な確率密度関数の一つである．

　さまざまな確率密度関数を図8に示します．定義式や平均，分散のほか，各確率信号から得られたヒストグラムを正規化したものも示しています．正規化したヒストグラムが近似的に確率密度関数を表していることが確認できます．

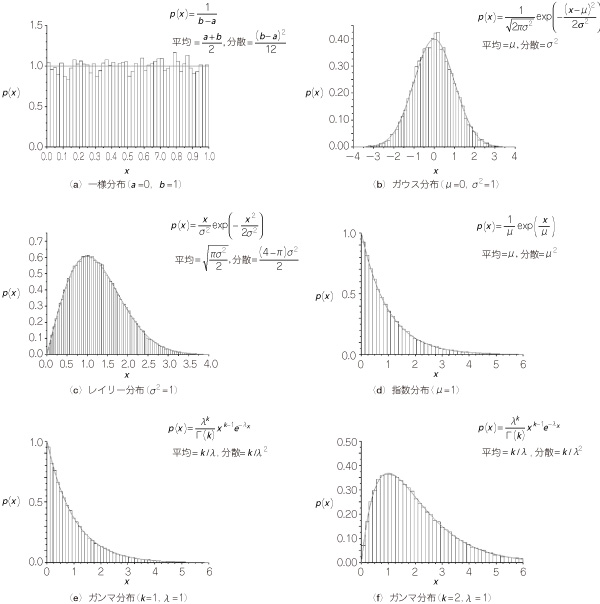
図8　いろいろな確率密度関数とそのヒストグラム
定義式や平均，分散のほか，各確率信号から得られたヒストグラムを正規化したものも示している．