音声信号処理の基礎理論（後編） ―― 線形フィルタ，適応アルゴリズム，周波数領域の処理

音声圧縮，ノイズ除去，音源分離などの音声処理で用いられている理論について説明する解説記事の後編です．ここでは，線形フィルタや適応アルゴリズム，周波数領域の関数処理などに述べます．数式を用いた理論の学習はやや退屈な面もありますが，これを理解しておけば，さまざまな音声処理をハードウェア化，ソフトウェア化する際の理解度が上がるはずです． （編集部）

※ 本記事は，ディジタル・デザイン・テクノロジ No.6から転載いたしました．同誌はこちらから購入できます．

2．線形フィルタ

● 線形時不変（LTI）フィルタ

　時刻nの信号x₁(n)，x₂(n)に対するあるディジタル・フィルタの応答がそれぞれy₁(n)，y₂(n)であったとします．もし，任意の実数a，bと，任意の整数τについて，

...(20)

に対する同じフィルタの応答が，

.....(21)

であるならば，そのフィルタを線形時不変（LTI）フィルタと呼びます（図20）．

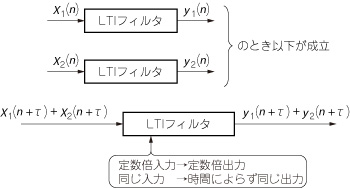
図20　LTI フィルタ

　LTIフィルタは，信号処理の分野における基本的なフィルタであり，低域通過フィルタ，高域通過フィルタ，帯域通過フィルタなどの一般的なフィルタの設計や，システム同定によるノイズ除去を考えるときに用いられます．

● LTIフィルタの一般形

　信号処理で用いる基本的なフィルタは，図21に示す三つの要素だけで構成されます．加算器は複数の入力信号を加算します．乗算器は入力信号に乗算係数を乗じたものを出力します．遅延器は入力信号を1時刻だけ遅延させます．

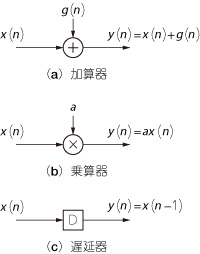
図21　フィルタの3要素
加算器は複数の入力信号を加算する．乗算器は入力信号に乗算係数を乗じたものを出力する．遅延器は入力信号を1時刻遅延させる．

　LTIフィルタの一般的な形を図22に示します．

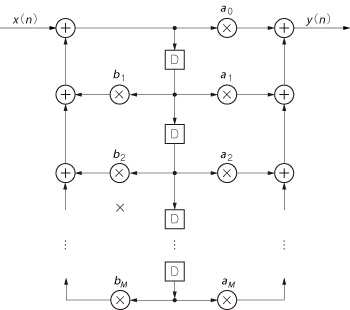
図22　LTI フィルタの一般形
フィルタ係数a_m，b_mが時間によらず一定．

　LTIフィルタでは，フィルタ係数a_m，b_mが時間によらず一定でなければなりません．ただし，適応フィルタでは，フィルタ係数を各時刻で更新するので，係数がある値に収束した後にLTIフィルタとして働くことになります．

● インパルス応答と周波数特性

　インパルス信号をLTIフィルタに入力したときの出力をインパルス応答と呼びます（図23）．インパルス応答を知れば，任意の値が入力されたときのLTIフィルタ出力を計算できます．

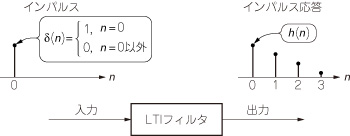
図23　インパルス応答
インパルス信号をLTIフィルタに入力したときの出力をインパルス応答と呼ぶ．

　例えば，n＝0に2が入力されると，その出力はインパルス応答を各時刻でそれぞれ2倍したものになります．
　インパルス応答の離散時間フーリエ変換は次式で与えられます．

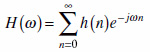.....(22)

　H(ω)を，LTIフィルタの周波数特性と呼びます．周波数特性H(ω)は複素数で与えられるから，

.....(23)

のように絶対値｜H(ω)｜と偏角∠H(ω)で表現できます．ここで，｜H(ω)｜を振幅特性，∠H(ω)を位相特性と呼びます．また，それぞれの具体的な値を振幅スペクトル，位相スペクトルと呼びます．

　周波数領域のノイズ除去では，人間の聴覚が位相よりも振幅の変化に敏感であることを考慮して，振幅スペクトルだけに着目して処理を行うことが多くなります．