音声信号処理の基礎理論（前編） ―― 音声圧縮，ノイズ除去，音源分離で用いられる理論

● 時間平均

　1回の試行で一つの確率信号が得られるのではなく，図14のように，1回の試行で一つのつながりの時系列として確率信号が得られる場合を考えます．

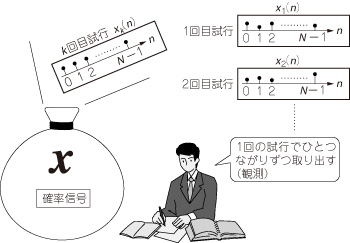
図14　時系列で得られる確率信号のイメージ
1回の試行で一つのつながりの時系列として確率信号が得られる場合を示している．

　k回目の試行における時刻nの実現値をx_k（n）とすると，時間平均は次式で定義されます．

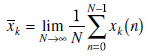　　 .....(5)

　時間平均も期待値と同じように無限の観測結果から得られます．これらは混同しやすいので注意が必要です．

　時間平均と期待値の違いを図15に示します．

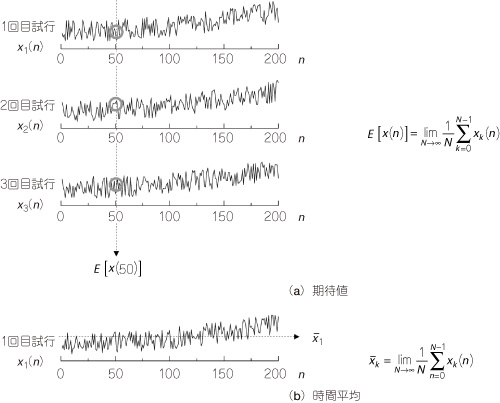
図15　期待値と時間平均
期待値は試行方向の平均，時間平均は，試行回数ごとに定義される．

　ここで，1回の試行で単位時間ごとに連続して値が得られるとします．期待値は試行方向の平均ですから，図15(a)に示すように，各時刻nについてそれぞれ定義されます．

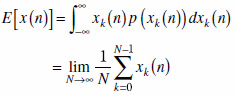　　 .....(6)

　一方，時間平均は，時刻nとは無関係な値になります．図15(b)に示すように，試行回数kごとに定義されます．

　従って，各時刻において確率信号が従う確率分布が異なる場合，時間平均と期待値は一致せず，時間平均はあまり意味を持ちません．各時刻において確率分布が変化しない確率信号に限り，時間平均と期待値は一致します．

● エルゴード過程

　信号処理の対象となる観測信号は，たった1回しか手に入らないことも多く，この場合には期待値を求めることはできません．そこで，期待値と時間平均が一致すると仮定し，期待値を時間平均で代用することがあります．つまり，

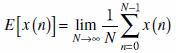　　 .....(7)

が成立するような場合です．このような性質を持つ信号系列をエルゴード過程と呼びます．

　信号処理では，多くの場合，処理対象となる確率信号がエルゴード過程であると仮定して扱います．

● 共分散と無相関

　図13で示したように，確率信号x₁の平均をμ₁とするとき，x₁の平均値からの散らばりの程度を表す分散は，

　　 .....(8)

で定義されます．

　これに対し，確率信号x₂の平均値をμ₂として，x₁とx₂の平均値からのずれの積の期待値，つまり，

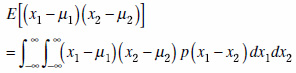　　 .....(9)

を分散との対比から，x₁とx₂の共分散と呼びます．共分散は，x₁とx₂が同じタイミングで同じ値（すなわちx₁＝x₂）となるときに最も大きくなります．このため，信号の関連性を調べるときに有用です．

　もし共分散が0，すなわち，

　　 .....(10)

ならば，x₁とx₂は無相関であるといわれます．これは，E［x₁x₂］＝E［x₁］E［x₂］と同じ意味です．

　わたしたちが扱う信号は，あらかじめ平均値を差し引き，平均値を0とすることがよくあります．この場合は，無相関の条件を簡単に，

　　 .....(11)

と書くことができます．

● 独立

　複数の確率信号を扱う場合，それらの和の期待値は，個々の期待値の和に等しくなります．つまり，M個の確率信号の和の期待値は，
　　
　　 .....(12)

のように別々に扱うことができます．

　一方，M個の確率信号の積の期待値は，個々に扱うことができず，

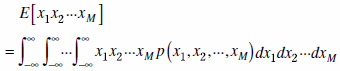　　 .....(13)

のように結合確率密度関数を考えなければなりません．ここで，結合確率密度関数が，

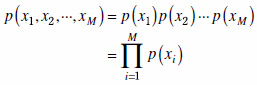　　 .....(14)

のように書けるならば，確率信号x₁，x₂，...，x_Mは互いに独立であるといわれます．

　容易に分かるように，複数の確率信号がそれぞれ独立である場合には，

　　 .....(15)

が成立するので無相関でもあります．ただし，その逆は必ずしも真ではありません．つまり，無相関は式(14)が成立しなくとも起こります．