FPGAを使った数値演算回路実現の勘所(4) ―― 浮動小数点演算器の構成を考える Part 2

●シフタの実現について

　浮動小数点演算においては，「固定小数点→浮動小数点」，「浮動小数点→固定小数点」の変換，あるいは正規化などの操作においてシフタ機能が必要になります．「固定小数点→浮動小数点」の場合は先頭の1を見つける機能と同居する必要があるので除くとしても，それ以外の場合は，「多入力→1出力」のマルチプレクサが使用されます．これを効率的に実現できることは，浮動小数点回路の実現に大きく寄与します．

　Xilinx社のSpartan 3ではLUTが4入力を前提としているので，2：1のマルチプレクサしか実現できません．ただし，スライス内の専用マルチプレクサを使えば，LUTを併用して4：1，8：1のマルチプレクサを実現できます．図3にその構成法を示します．

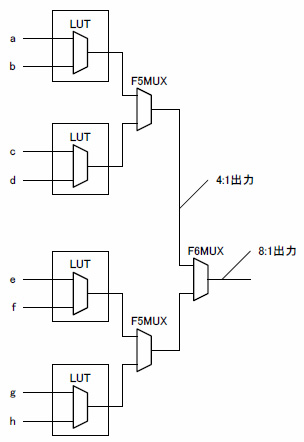
図3　専用マルチプレクサ使用による多対1マルチプレクサの構成

　ところが，シフタを構成するに当たり必要とされるマルチプレクサの構成は図4に示すようなもので，各段で必要とされる2：1マルチプレクサの数は1：1の関係になっています（図4は最大シフトアップ＝7の場合の例）．

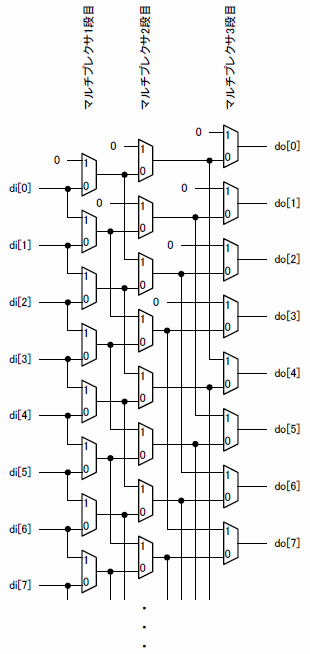
図4　シフタで必要とされるマルチプレクサの構成

　ところが，先に述べた専用マルチプレクサのリソース数はLUTと1：1ではないため，シフタの実現には向いていません．従って，指数部の値に沿ったシフトを行う際には，少々もたつき感があります．

　これに対して，同じくXilinx社のVirtex-5やSpartan-6などでは，LUTが6入力を前提としています．4：1のマルチプレクサが1LUTで実現できるため，効率の良いシフタ実現が可能となります．所望のシフタを得ようとしたとき，通過するLUTの数がほぼ半分になるので，ありがたい構造と言えます．

　また，シフタを構成するにあたり，マルチプレクサの制御の方法については注意が必要です．図4に見られる構造は，1段目のマルチプレクサの制御をシフト変数の下位ビットから割り当てた場合を想定していますが，上位ビットから割り当てる構成法をとることも可能です．機能的に等価なものが得られますが，回路規模に差が出ます．

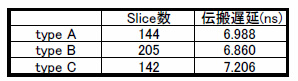
　表1は，入力変数を24ビット，シフト変数を6ビットとして単純なアップ・シフタを記述し，Spartan-3（xc3s50-5pq208）をターゲットとしてXSTにて論理合成した場合のSlice数と伝播遅延を示しています．

表1　記述の違いと論理合成結果

　type Aは1段目のマルチプレクサの制御をシフト変数の下位ビットから割り当てた場合，type Bは逆に上位から割り当てた場合，type Cは具体的な割り当てを明示せず，シフト演算子でシフト変数分をシフトアップするように記述した場合です．type Aとtype Bで回路規模に差が出る理由を図5に示します．一目瞭然ですね．

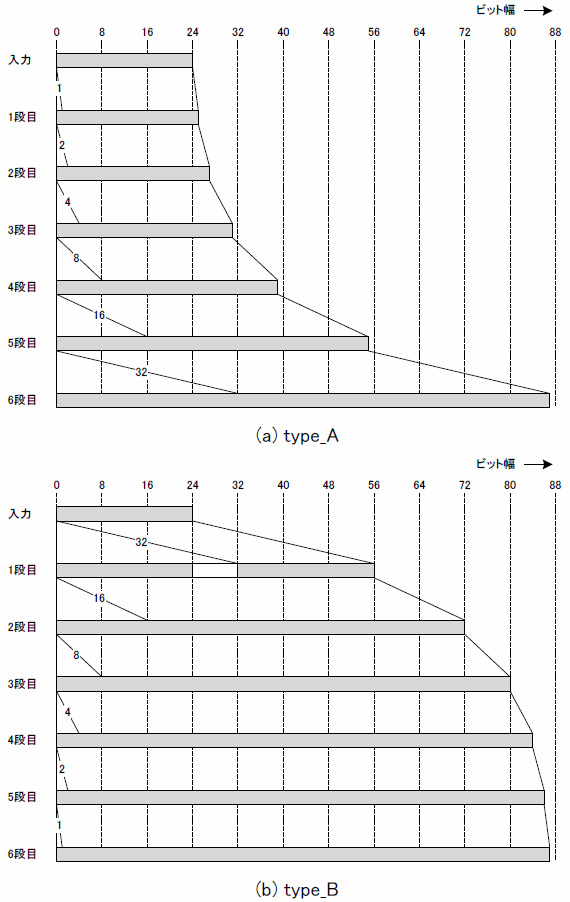
図5　アップ・シフタの制御による構成の違い

　type Cはtype Aとほぼ同等の結果となっています．XSTがうまくやってくれたというところでしょう．また，伝播遅延には大きな差はなく，配置配線によるばらつきの範囲内となっています．

　　　　　　　　　　　　　　　＊　　　　　　　　　　　　　　　＊　　　　　　　　　　　　　　　＊

　前回と今回の2回に分けて，浮動小数点演算回路の基礎とFPGAにおける実現について説明しました．要するに，規格にとらわれずに実現する方法もあるのですよ，ということが言いたかっただけなのです．

　実現すべきシステムの要求のもとで，より効率的に実現するための抜け道はまだまだあるはずですが，それは要求によって変わるので，一概に言えるものではありません．感性を研ぎ澄まして，より良い抜け道を探してみてください．できれば，何らかの形で紹介していただければ，ありがたいと思います．

参考文献
(1) 鈴木 昌治；ディジタル数値演算回路の実用設計，CQ出版，2006年．
(2) Xilinx社；Spartan-3ジェネレーションFPGAユーザーガイド．
(3) Xilinx 社；Spartan-6 FPGA コンフィギャブルロジックブロックユーザーガイド．
(4) Xilinx社；Virtex-5 FPGA User Guide．
(5) Xilinx社；Virtex-6 FPGA コンフィギャブルロジックブロックユーザーガイド．

すずき・しょうじ