FPGAを使った数値演算回路実現の勘所(4) ―― 浮動小数点演算器の構成を考える Part 2

●最大誤差を推定して丸めを省く

　演算を何度も繰り返す場合は別として，演算の深さがそれほどではなく，丸めを省いた場合の誤差が確定でき，その精度で問題ない場合は，丸めを省いても構わないと考えましょう．重要なのは規定されたフォーマットを守ることでなく，アプリケーションに必要な精度を守ることです．

●例外が発生しないようにして例外処理を省く

　例えばNaNや∞（オーバフロー）などの例外が，信号処理などで発生したらどうしますか？ 前値保持などを仕方なく適用しますか？

　これらの例外は，本来，あってはならないとされるアプリケーションは少なくありません．逆に，与えられるデータをシステムとして正しく管理しさえすれば，そうした例外を回避できる場合も少なくありません．それが実現可能とすれば，演算回路側では例外処理を省くことができます．これも回路コストを下げる有効な手段です．本来，例外処理というのは，演算回路だけで対応するべきことではないので，システム全体での考慮が必要です．

　また，オーバフローについて補足すれば，演算による結果の値の範囲を確定できれば，オーバフローが起きないように値を管理できるアプリケーションは少なくないと覚えておきましょう．設計者の怠慢で値の範囲が確定できないことになっている，というケースは意外と多いものです．

　もし，値の範囲を確定できるのであれば，それに合わせた指数部を用意すればよいことになります．値の範囲を確定できない場合は，指数部を1けた増やしてしまうというのも一つの手段としてありますが，このあたりの手抜きはあまり褒められたものではありません．後で痛い目に会ったりするので，お勧めしません．なぜなら，指数部を1けた増やすことで事足りる，という保証がないからです．

●オリジナル浮動小数点フォーマットを採用する

　さて，ここからはFPGA特有の話になります．

　すでに，｢システムが要求する精度を考慮することが必要だ｣という話はしました．逆に，ハードウェアで実現できる上限の精度で仕様が満たせるのなら，それを浮動小数点フォーマットとするのも一つの方法です．

　例えば，Xilinx社のSpartan-3で使用できるハード・マクロ乗算器は，符号付き18ビット×符号付き18ビットです．符号なしの仮数部を乗算するとすれば，符号なし17ビット×符号なし17ビットが上限となります．仮数部が暗黙の1を加えて17ビットで足りるのであれば，これを仮数部のフォーマットとして採用するのも一つの方法でしょう．ただし，要求精度からかけ離れてしまい，過剰精度にならないように注意しましょう．

●除算コアにテーブルを用いて，浮動小数点のうま味を利用

　除数入力が正規化数である（非0は必須）と限定されれば，

　1 ≦ 除数の仮数部 ＜ 2

より，

　0.5 ＜ 1 / 除数の仮数部 ≦ 1

となり，逆数演算の仮数部そのものは範囲の限定された演算となります．指数部は符号を反転させるだけです．ここから，「テーブル＋補間演算」による近似によって，逆数演算を比較的簡単に得ることができます．

　図1に「テーブル＋直線補間」による逆数演算のブロック図を示します．入力変数を16ビットとし，上記区間を32分割してテーブルを作成した場合の例です．

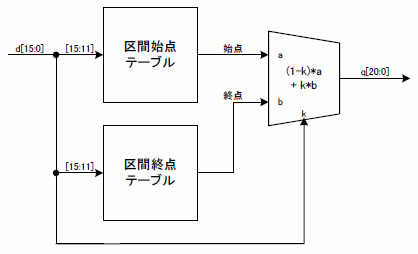
図1　「テーブル＋直線補間」による逆数演算のブロック図

　図2には，より高精度を期待する場合として，2次誤差補正を加えた場合の例を示します．具体的な実現方法については，参考文献(1)を参照してください．

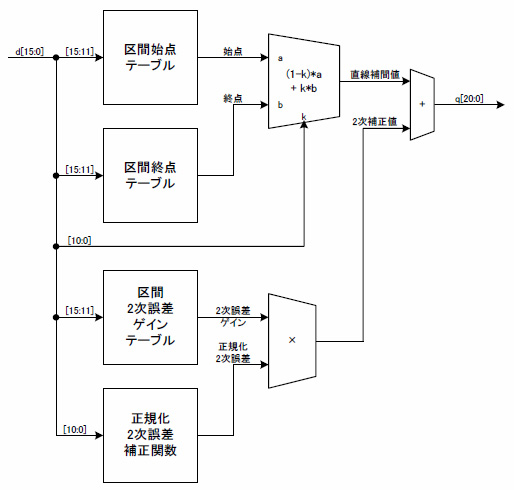
図2　2次補正追加による逆数演算のブロック図

　昨今のFPGAは内部にメモリを潤沢に抱えているので，テーブルは容易に実現できます．得られた除数の逆数に被除数を乗算すれば，除算が実現できます．除数の逆数演算と被除数の乗算を終えてから正規化や丸めを行えば，後処理も1回で済みます．回復法のような逐次演算を何度も繰り返す方法よりも，FPGAにおいては手っ取り早い除算法といえるでしょう．