音声信号処理の基礎理論（後編） ―― 線形フィルタ，適応アルゴリズム，周波数領域の処理

3．適応アルゴリズム

　LTIフィルタとは異なり，与えられた手順に従って，フィルタ係数を更新し，自動的に所望の特性を実現するフィルタがあれば便利です．このようなフィルタを適応フィルタと呼びます．また，係数更新の手順を適応アルゴリズムと呼びます．

　適応アルゴリズムは多くの場合，フィルタ出力と所望の信号との2乗平均誤差が最小となるように設計されます．所望の信号をd(n)，フィルタ出力をy(n)，それらの差をe(n)としたとき，2乗平均誤差を評価関数Jとして次式で定義します．

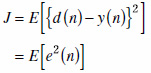.....(24)

　適応フィルタを図27のようにFIRフィルタで構成するものとします．

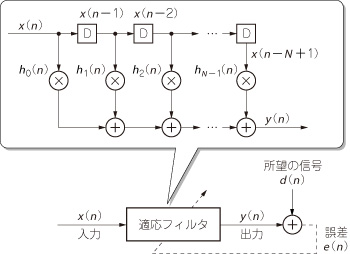
図27　適応フィルタの構成
FIRフィルタで構成した例を示す．

　このとき適応フィルタの出力は次式で与えらます．

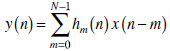.....(25)

　式(25)を式(24)に代入すれば，評価関数Jは，各フィルタ係数の2次関数となることが分かります．

　これを視覚的に確認するため，次数N＝2のときの評価関数Jのイメージを図28(a)に示します．

　評価関数Jを最小化するためには，Jを各フィルタ係数で偏微分し，その関数の傾きと逆符号の方向にh_mを更新します．この様子を図28(b)と図28(c)に示します．

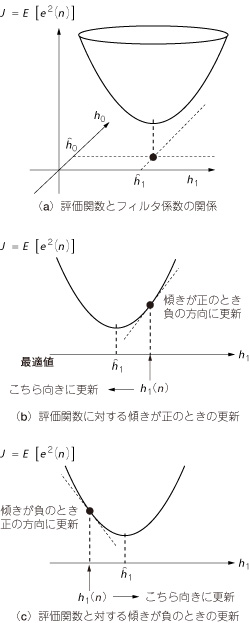
図28　評価関数と係数更新
評価関数Jを最小化するためには，Jを各フィルタ係数で偏微分し，その関数の傾きと逆符号の方向にh_mを更新する．

　さて，フィルタ係数を「定数」と考えて，実際にJを偏微分すると，

.....(26)

という簡単な式が得られます．これがフィルタ係数h_mに対するJの傾きですから，式(26)と逆符号の向きにフィルタ係数を更新します．更新の大きさを決める正の量μ/2を導入して，h_m(n)に関する適応アルゴリズムを書くと，

.....(27)

が得られます．ここで，μはステップ・サイズと呼ばれます．

　式(27)は最急降下法と呼ばれる適応アルゴリズムです．ただし，μの値が大きすぎると係数が発散するので，その設定には注意が必要です．また，実際には期待値は計算できないことにも注意します．そこで実際の応用では，更新項を瞬時値としたLMSアルゴリズムがよく用いられます（図29）．

図29　LMSアルゴリズムとNLMSアルゴリズム