音声信号処理の基礎理論（後編） ―― 線形フィルタ，適応アルゴリズム，周波数領域の処理

● FIRフィルタとIIRフィルタ

　図22において，フィルタ係数b_mがすべて0の場合を考えます．これを図24に示します．

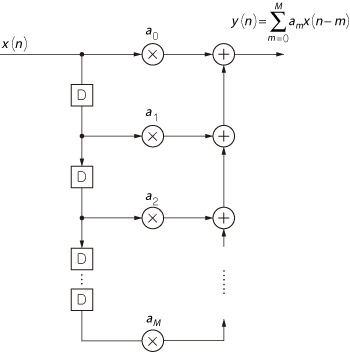
図24　FIR フィルタ
フィルタ次数が有限であれば必ず有限長でインパルス応答が終了する．

　このフィルタのインパルス応答は，a₀，a₁，…，a_Mとなり，フィルタ係数が順番に現れます．従って，フィルタ次数が有限であれば必ず有限長でインパルス応答が終了します．このことから，FIRフィルタと呼ばれます．

　一方，いずれかのb_mが値を持つとき，FIRフィルタとはなりません．例として図25のフィルタのインパルス応答を調べると，1，b₁，b₁²，b₁³，…となりb₁のべきが無限に続くことが分かります．そこでこのようなフィルタは，IIRフィルタと呼ばれます．

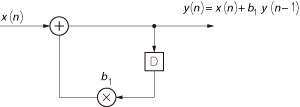
図25　IIR フィルタ
1次の例を示す．インパルス応答が無限に続く．

　FIRフィルタは必ず安定な出力が得られますが，IIRフィルタはフィルタ係数の与え方によっては出力が発散するため，その設計には注意が必要です．

● Scilab演習 —— LTIフィルタを作る

　LTIフィルタにより，低域通過フィルタ，高域通過フィルタ，帯域通過フィルタを作成し，音声を通過させてみましょう．ただし，フィルタ次数はすべて31とし，低域通過フィルタと高域通過フィルタのカットオフ周波数は0.3π，帯域通過フィルタのカットオフ周波数は，0.1πと0.3πとします．

　各種フィルタを実現するScilabのプログラムをリスト2に示します（Scilabで使用するプログラムやデータは，こちらのWebページからダウンロードできる）．ここではScilabに組み込まれている関数を利用して作成しています．

リスト2　Scilabによるフィルタのプログラム

　低域通過フィルタのシミュレーション結果を図26に示します．

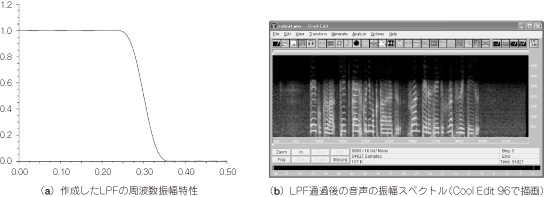
図26　Scilabで作成した低域通過フィルタ

　低域通過フィルタと高域通過フィルタはカットオフ周波数（0.3π）を一つ設定するだけです（［0.3 0］の後ろの0は無視される）．

　帯域通過フィルタを実現する場合は，カットオフ周波数を二つ設定します．［0.1 0.3］という設定では，低域側が0.1π，高域側が0.3πとなります．