音声信号処理の基礎理論（後編） ―― 線形フィルタ，適応アルゴリズム，周波数領域の処理

4．周波数領域の処理

● 離散フーリエ変換（DFT）

　計算機において，時間領域で得られた信号を周波数領域へ変換する方法として，離散フーリエ変換（DFT）が用いられます．

　範囲0≦n＜Nにのみ値を有する信号x(n)に対するDFTと逆DFT（IDFT）は図30のように定義されます．

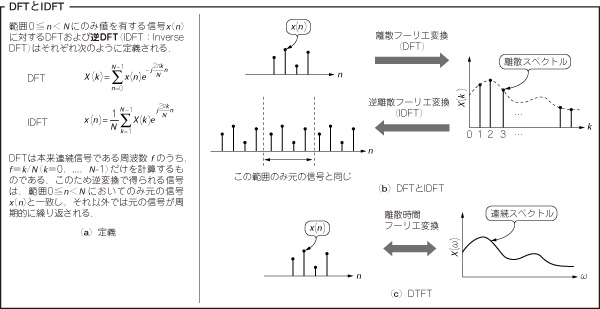
図30　離散フーリエ変換の違い
DFTとIDFTの関係や，離散時間フーリエ変換との違いを示す．

　DFTは離散スペクトルだけを持つので，計算機に適しており，さらに高速算法が存在するという利点があります．

● 窓関数

　音声信号を対象としてDFTを計算する場合，フレーム長を，音声が定常と見なせる30ms前後に設定することがよくあります．このため，適当な窓関数によって30ms前後の信号を切り出す必要があります．

　フレーム長をNとすると，窓関数は，0≦n≦N−1において有限値をとり，それ以外で0となる関数として定義されます．これまでにさまざまな窓関数が提案されています．

　代表的な窓関数を図31に示します．ただし窓長N＝256としてプロットしています．

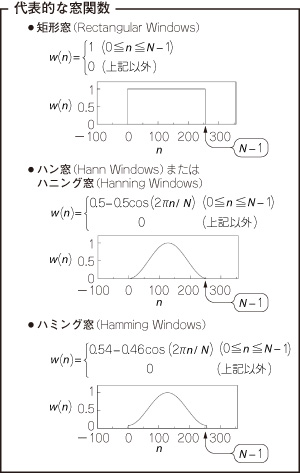
図31　窓関数
0≦n≦N−1において有限値をとり，それ以外で0となる関数である．

● ハーフ・オーバラップ

　窓関数で切り出した音声信号に対して，DFT⇒信号処理⇒IDFTとして処理後の音声を得る場合がよくあります．ところが，音声処理でよく用いられるハン窓（図31）では，切り出された音声信号の両端は減衰しています．このため，DFＴ→IDFTとして元の信号に戻してもフレーム両端の音声は減衰したままになってしまいます．そこで，フレーム長の半分だけ時間をシフトして次のDFTを実行し，得られた結果を前のフレームで得られた結果に加算する，ハーフ・オーバラップが用いられます（図32）．

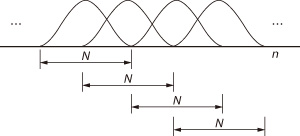
図32　ハーフ・オーバラップ
フレーム長の半分だけ時間をシフトして次のDFTを実行し，得られた結果を前のフレームで得られた結果に加算する．

　ハーフ・オーバラップにより，窓関数による減衰の影響をほとんど取り除くことができます．

● Scilab演習 —— ハーフ・オーバラップの実装

　音声に対してハーフ・オーバラップを実行してみましょう．フレーム長を256サンプルとして，フレーム・シフトを128サンプルとします．また，窓関数にはハン窓を用います．

　Scilabのプログラムをリスト3に，結果を図33に示します．

リスト3　Scilabによるハーフ・オーバラップのプログラム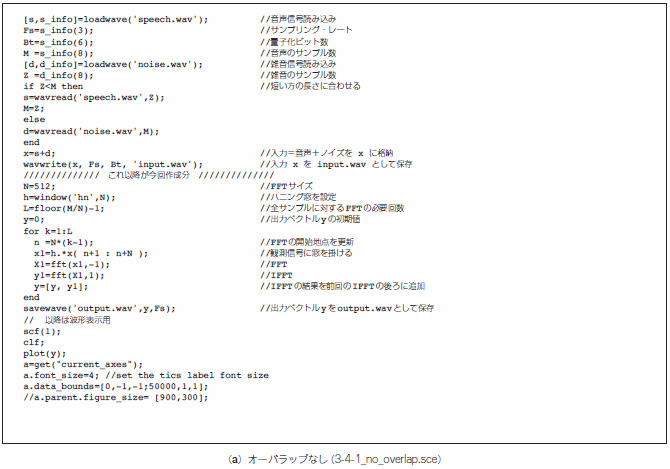



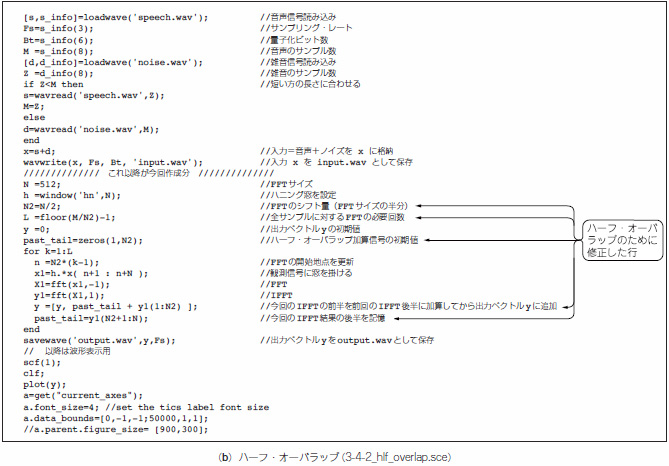
図33　Scilabによるハーフ・オーバラップのシミュレーション結果
フレーム長を256サンプルとして，フレーム・シフトを128サンプル，窓関数としてハン窓を使用した例を示す．

参考・引用*文献
(1) 村田 昇；入門 独立成分分析，東京電機大学出版局，2004年．
(2) 飯國 洋二；基礎から学ぶ信号処理，培風館，2004年．
(3) 古井 貞熙；ディジタル音声処理，東海大学出版社，1985年．
(4) サイモン ヘイキン（著），武部幹（訳）；適応フィルタ入門，現代工学社，1987年．

かわむら・あらた
大阪大学大学院 基礎工学研究科 システム創成専攻 助教
おち・ひろし
九州工業大学大学院 情報工学研究院 電子情報工学研究系 教授