インテグリティな技術コラム(4) ―― ラプラス変換からフーリエ変換へ

● 周波数特性から過渡応答を求める

　...というタイトルにしていますが，厳密には周期関数を加えた際の時間応答です．式(9)の電圧源をパルス波形とします．パルス波形を周波数関数で表す際にフーリエ変換を用います．図5は簡単な台形波です．これをフーリエ変換するには，式(付3)を用います．折れ線の関数なので，一応求めることは出来ますが，やや煩雑です．稿末の付録に計算経過を記載したので，興味のある人は確認してみてください．それよりも，ラプラス変換して，s→ｊωと置いて周期Tで割ってフーリエ変換を求めるほうがずっと簡単です．

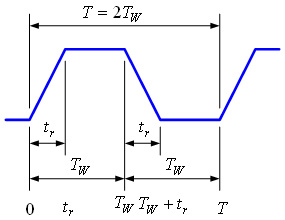
図5　パルス波形

　図5の台形波（パルス波形）はランプ波形の繰り返しです．時刻t＝0において正のランプ波形，t＝t_γで負のランプ波形，t＝T_wで負，t＝T_w＋t_γで正，単にこれだけです．

　立ち上がり時間がt_γの振幅1のランプ波形は，

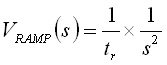.........(10)

　時間遅れは，

.........(11)

　用いるラプラス変換はこの二つだけです．したがって，図5の波形のラプラス変換は，

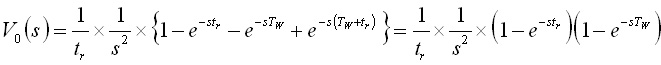.........(12)

となります．ここで，フーリエ変換にもっていくために，s→ｊωと置いて周期Tで割ります．

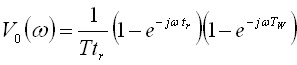.........(13)

と，ここまででもいいのですが，オイラー（Euler）の公式e^jx＝cos x＋j sin xを用いて，

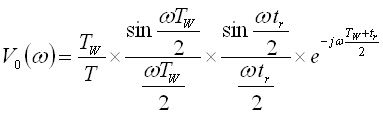.........(14)

となり，イメージしやすい形になりました．右辺のsin x / xはsinc関数と呼ばれるもので，最後の因子はe^-jωτの形をしており，単なる時間遅れを表しています．

　式(14)を式(9)の信号源V₀(ω)に代入すると，出力電圧V(ω)が求まります．この周波数関数を高速フーリエ変換（FFT：Fast Fourier Transform）すると，時間応答が得られます．

　FFTは例えば，Excelなどの表計算ソフトウェアにも組み込まれているので利用できます．ただし，使い勝手はお世辞にもよいとは言えません．Excelで複素数を取り扱うには，エンジニア関数を用います．例えば，加算はimsum，減算はimsubなどです．Excelシートで，「挿入」→「関数」→「エンジニア」の順で探してください．各セルはx＋j yの形であり，テキストの属性で表されます．サンプルのExcelシートでやり方を習得してください．
　
・Excelシートのダウンロード　
※ダウンロードするには，CQ出版のサポート・サイト「CQ connect」への登録が必要です
　
　Excelに組み込まれているFFTは，上述のように使い勝手がよくありません．もう少し簡単に使えるFFTを筆者が作成していますが，これは別の機会に紹介したいと思います．

● 反射の解析をFFTで

　前回のラプラス変換による分布定数の解では，遠端の電圧をラプラス変換によって，

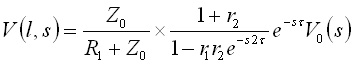.........(15)

と求めました．r₁およびr₂は近端と遠端それぞれの反射係数で，

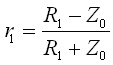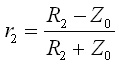， .........(16)

でした．これらを用いて，式(15)のV₀の係数（伝達関数）を書き直すと，

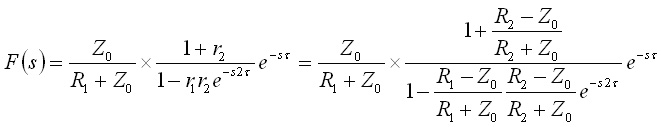
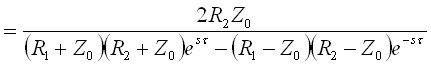.........(17)

を得ます．ここで，s→jωと置くとフーリエ変換となります．すなわち，

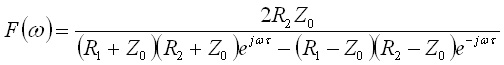.........(18)

となって，これが線路の周波数特性です．式(18)と式(14)の積により遠端の電圧が求まります．オイラー（Euler）の公式e^jx＝cos x＋j sin xを用いると，式(18)は，

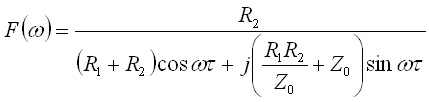.........(19)

と書き換えられます．式(19)と式(14)の積をフーリエ逆変換して遠端の電圧vを求める方法も，先ほどのサンプルのExcelシートに掲載しているので，ご覧ください．

　なお，サンプルのExcelシートのFFTは128点です．分解能を上げたい方は，1024点以上にトライしてみてください．

うすい・ゆうぞう
シグナル インテグリティ コンサルタント
http://home.wondernet.ne.jp/~usuiy/

◆筆者プロフィール◆
碓井 有三（うすい・ゆうぞう）．1972年，富士通株式会社入社．回路技術部長，テクノロジ本部主席部長などを経て，2001年に退社．同年，株式会社マクニカ入社．同社CTOなどを経て，2008年退社．現在，フリーのコンサルタント．