インテグリティな技術コラム(3) ―― ラプラス変換による分布定数の解

●境界条件と係数方程式

　微分方程式の一般解に図2の境界条件を入れて，積分定数を求めます．

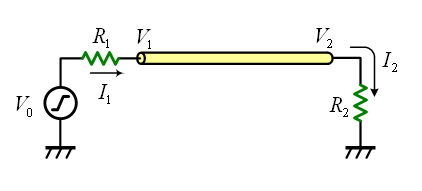
図2　境界条件

　近端（x＝0）は，

の関係があります．式(6)および式(7)にx＝0を代入すると，近端の電圧と電流は，

なので，これらを式(12)に代入して，

を得ます．

　遠端（x＝l）の境界条件は，

です．遠端の電圧と電流は，式(10)および式(11)にx＝lを代入して，線路の片道の伝搬遅延時間をτとすると，

なので，

 となります．式(16)に式(18)と式(19)を代入して，

を得ます．式(15)および式(20)はA₁(s)とA₂(s)とに関する連立方程式です．このA₁(s)およびA₂(s)は式(10)および式(11)の係数なので，この連立方程式を解くと，任意の場所の電圧と電流を求めることが出来ます．

　さて，式(15)と式(20)を，A₁(s)とA₂(s)について解きます．未知数が二つなので，どんな方法でも簡単に解けますが，ここでは行列式を使って解きましょう．

　まず，行列表記すると，

となります．次に係数の行列式を求めます．

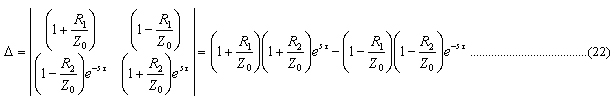
　A₁，A₂は，

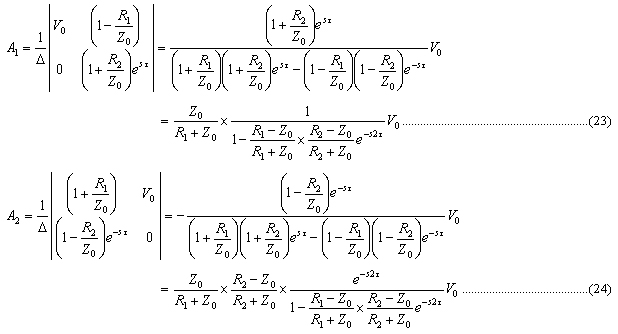
 と求まりました．近端と遠端それぞれの反射係数r₁およびr₂は，

なので，式(23)および式(24)は，

となります．

　式(26)および式(27)を式(10)に代入すると，

 が得られました．式(28)および式(29)をラプラス逆変換すると，時間応答が得られます．