インテグリティな技術コラム(3) ―― ラプラス変換による分布定数の解
●微分方程式の解
式(4)の最初の式をもう一度xで微分して,式(2)を代入すると,
![]()
となります.
式(5)は2階の微分方程式では最も簡単な斉次形で,一般解は,
![]()
と求まります,A1,A2は積分定数です.式(6)を式(4)の最初の式に代入すると電流が求まります.
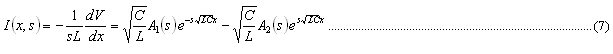
ここで二つのパラメータを定義します.一つは,
![]()
で,もう一つは,

です.uは信号の進む速度で,Z0は特性インピーダンスです.これらを用いて,式(6)および式(7)を書き換えると,
![]()

となります.各指数の肩は,距離を速度で割るので,時間のディメンションになります.


