インテグリティな技術コラム(11) ―― クロストーク・ノイズと二つの異なる伝送モード

●コモンとディファレンシャルの二つのモードで伝搬

　これは何を意味しているかというと，2本の線路の信号の，平均と，差の半分の波形が伝わっており，それぞれが異なる特性インピーダンスと異なる伝搬遅延とを有しているということです．線長が15cmなので，単位長当たりの遅延時間に直すと，それぞれ6.7ns/mと6.4ns/mとなります．この二つの波形がコモンv_Cとディファレンシャルv_Dです．よって，以下のようになります．

..... (7)

..... (8)

　加害者の線路はコモンとディファレンシャルとの和，被害者はそれらの差の信号となることが分かります．コモンとディファレンシャルは，それぞれ特性インピーダンスZ_CとZ_D，および伝搬遅延t_dCとt_dDを有します．

●クロストークを計算で求める

　ここで，図4(a)のように，2本の線路に，それぞれ等しい＋1/2の信号を加えた場合を考えます．回路は完全に対称なので，v₂＝v_Fとなります．式(7)および式(8)にこの条件を入れると，v_D＝0，すなわちコモンだけが伝搬していることが分かります．同じように，図4(b)の場合は，2本の線路に符号の異なる＋1/2と－1/2の信号を加えた場合だと，v₂＋v_F＝0になるので，v_C＝0，すなわちディファレンシャルの波だけが伝搬します．したがって，コモンとは文字どおり，2本の線路で同じ極性の信号が伝搬するモード，ディファレンシャルとは逆極性の信号が伝搬するモードであることが理解できたと思います．

図4　二つのモード

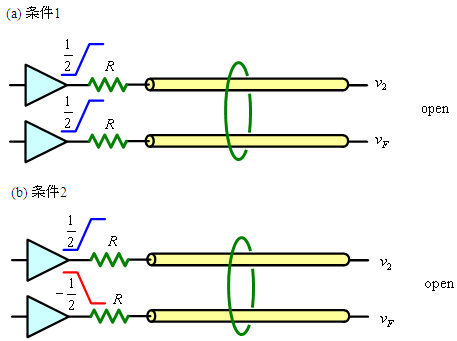
　さて，図4の遠端の信号v_Fをそれぞれ求めます．それぞれのモードの特性インピーダンスZ_CとZ_Dを用いて，信号にもCとDのサフィックスをつけると，以下のようになります．

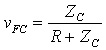..... (9)

..... (10)

　ここで，これらの式の両辺を加えると，以下の式が得られます．

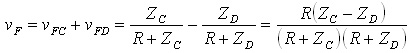..... (11)

　下側の線路は，信号源が＋1/2と－1/2であったので，重ね合わせると信号源がなくなる，すなわち何も信号を加えてない線路に式(11)の信号が現れることを意味します．式(11)が，図2の被害者の信号v_Fです．

●基礎クロストーク係数を導入

　ここで，新たな概念として，式(12)で定義される基礎クロストーク係数ξを導入します．

..... (12)

　2本線路の公称の特性インピーダンスZ₀は，Z_CとZ_Dの幾何平均，すなわち以下の式で表されます．

..... (13)

　式(12)および式(13)を用いると，以下のようになります．

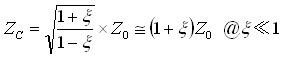..... (14)

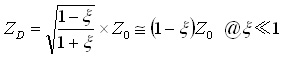..... (15)

　ξが十分に小さいという条件で式(11)を変形すると，以下のようになります．

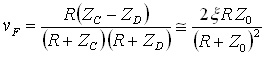..... (16)

　つまり，クロストークは基礎クロストーク係数ξに比例します．