音声の分析・合成処理の基本 ―― 携帯電話やVoIPで使われている音声圧縮技術の仕組み

●エンコーダにおける音声の分析方法

　分析合成方式のエンコーダ側では，ピッチ周期やパルスの大きさ，フィルタ係数などのパラメータを実際の音声から抽出しなければなりません．一般的には，音声を通過させるとその出力が音源波形となる線形予測器と呼ばれるフィルタが用いられます．

　線形予測器のフィルタ係数は，LPC係数と呼ばれ，音声合成フィルタを構成するために用いられます．なお，LPC係数を求めることを線形予測分析と呼びます．

　音源を出力する線形予測器と，音声を出力する音声合成フィルタは互いに逆フィルタの関係にあります（図3）．従って，LPC係数が得られれば，その逆フィルタである音声合成フィルタを簡単に構成できます．

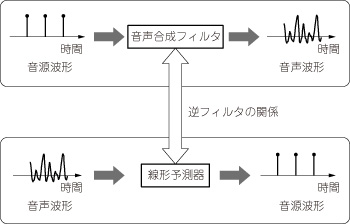
図3　音声合成フィルタと線形予測器との関係
音源を出力する線形予測器と，音声を出力する音声合成フィルタは互いに逆フィルタの関係にある．

●フィルタ係数を求める

　線形予測器と音声合成フィルタの構成を，図4に示します．

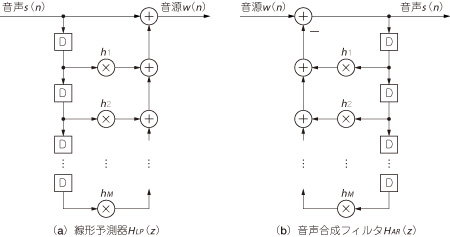
図4　線形予測器と音声合成フィルタの構成
h_m（m＝1，…，M）はLPC係数，s(n)は線形予測器への入力音声，w(n)は出力の音源情報．Dのブロックは1時刻の遅延を表している．

　LPC係数をh_m（m＝1，...，M）とし，線形予測器への入力音声をs(n)とすると，その出力w(n)は，

　　　　　(1)

で与えられます．ここでw(n)は音声の音源となっています．

　逆に，w(n)を入力とする音声合成フィルタ出力s(n)は，

　　　　　(2)

として計算されます．

　線形予測器の出力は音源w(n)ですから，ピッチ周期とパルスの大きさも線形予測器の出力から求めることができます．

　図4に線形予測器と音声合成フィルタを示します⁽²⁾．その伝達関数は，

　　　　　(3)

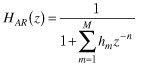　　　　　(4)

で与えられます．図4との対比からも分かるように，伝達関数とフィルタ構成には簡単な対応関係があり，いずれか一方から他方を導出できます．

　分析合成方式の音声圧縮では，このように音声の分析を行い，LPC係数と音源の情報（ピッチ周期，パルスの大きさなど）を符号化することで，波形符号化方式よりも高い圧縮率を実現しています．また，線形予測分析を用いて音声の符号化を実現するものを全般にLPCボコーダと呼ぶことがあります．

●Scilab演習 ---- LPC係数を求めて音声を合成する

　ここでは，男性が約1秒間連続音声した「あ」（8kHzサンプリング）に対して1回だけ線形予測分析を行ってLPC係数を求め，単純なパルス列を音源として音声を合成してみます．Scilabのプログラムをリスト1に示します．使用するデータはこちらのWebページからダウンロードできます．

リスト1　LPC係数を求めて音声を合成するプログラム（1-2-1_LPC.sce）

　LPC係数は音声の自己相関関数から得られます．その方法の一つにLevinson-Durbinのアルゴリズムがあり，lev関数としてScilabに標準で搭載されているので，今回はそれを使用します．

　まず，音声sを読み込み，次式で定義される自己相関関数を計算します．

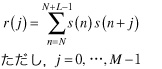　　　　　(5)

　ここで，音声「あ」をNサンプルからN＋Lサンプルまで分析することとし，自己相関の時間差を線形予測器の次数と同じMまでにする場合を示しています．リスト1では，①のように，N＝4000，L＝128，M＝14と設定しています．

　自己相関r(j)が計算された状態で，リスト1の②のようにlev関数を実行すると線形予測分析が行われ，13個（最初のLPC係数は常に1) のLPC係数がベクトルarに格納されます．また，sigma2には音源の振幅を2乗したものが格納されています．

　arを利用して設計した音声合成フィルタに，振幅がsigma2の平方根であるパルス列を入力し，1秒間の音声を合成します．ただし，音声合成に用いるパルスの間隔（ピッチ周期）は64サンプルとしています．

　式(2)に基づいて合成された音声波形を図5に示します．

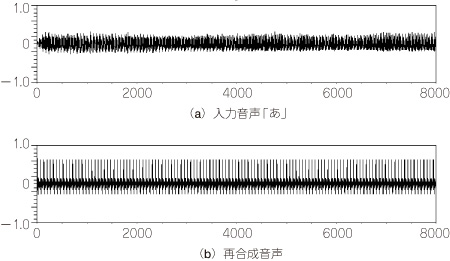
図5　LPC係数を求めて音声を合成するシミュレーション結果
「あ」として認識できる程度の性質は保持されている．

　結果として得られた音声を聞いてみると，1秒間の音声に対して1回だけの分析であるため，音声の自然性は損なわれているものの，「あ」として認識できる程度の性質は保持されていることが分かります．