暮らしに役立つ新QC七つ道具(3) ―― マトリックス・データ解析法：「要素間関係」を「要約」する

●複数の要素を主成分（合成変数）にまとめて，見通しをよくする

　マトリックス・データ解析法とは，大量のマトリックス・データを解析して，見通しのよい結論を得ようとする方法です．これは多変量解析^注1と呼ばれる解析法の一つで，統計学では主成分分析と呼ばれます． 

　主成分分析とは多くの変数を集約してまとめることで，それらが最終的にどういうことを表わしているのかを説明する方法です．マトリックス図法のみでは効果的な判断のできない場合で，数値データが存在している場合に使われます．

　以下，具体的な例で，説明してみましょう．

　例えば，「あなたが知っている一番おいしいラーメンのお店はどこか教えてください」といわれた場合，皆さんはどのような基準でその店を決めるでしょうか．

　ラーメンのスープが一番重要だと考える人もいれば，麺が一番重要だと考える人もいるでしょう．上にのっているチャーシューなどの具を重要視する人もいるかも知れません．

　これらの要素はみなラーメンのおいしさを決める要素です．一つの要素だけでは決めることができませんね．それに，それぞれの要素は同じような重要度ではないでしょうから，重要度に応じて評価を考えなければならないでしょう．では，店ごとにそれぞれの要素を5段階で評価した例を図1に示します．

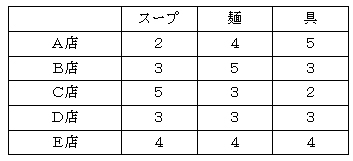
[図1]　各ラーメン店のラーメンを5段階で評価した例

　複数の要素が絡み合った場合，単純に比較できないことが分かります．このように複数の要素を持ったものに対して，どうすれば比較できるのでしょう？

　一つの考え方として，複数の要素があるから比較できないのだとすると，それらの要素を一つにまとめてしまえば比較できる，とする考え方があります．つまり，それぞれの要素に対して重要度を表わす数をかけて，全てを足すことで一つの数値としてまとめてしまい，それらを比べれば比較ができるのではないか，と考えたのが主成分分析（マトリックス・データ解析法）という技法です．

　一つの数値としてまとめられたものを合成変数といい，合成変数を作成することを変数の集約といいます．

合成変数 ＝ （A × スープ） ＋ （B × 麺） ＋ （C × 具材）

　この時の合成変数を主成分といい，A～Cを主成分負荷量といいます．A～Cは，合成変数が際限なく大きくなることを制限するために

という条件を持たせます．

　ここまでの説明で，そろそろ読むのがつらくなってきたでしょうか．（^ ^;

　マトリックス・データ解析法とはどんなものか，というのは，ここまでの概念が分かっていれば十分です．マトリックス・データ解析法の計算そのものはかなり面倒なものですが，ほとんどは表計算ソフトウェアで行うことができます．実際の計算方法まで説明すると，もう統計学の解説になってしまいますので，詳細について知りたい方は，統計学についての書籍^注2をご参照ください． 

　上記で説明した主成分は，第一主成分といいます．実際のマトリックス・データ解析法では，ここで説明した主成分（第一主成分）と第二主成分を調べてグラフ化することが一般的です（図2）．

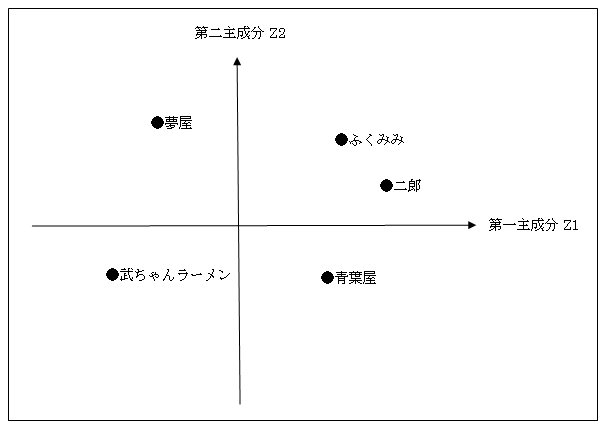
［図2]　マトリックス・データ解析法の例

＊                 ＊                  ＊

 　次回は「連関図法」を取り上げます．お楽しみに．（^ ^）

くにひろ・よういち

◆筆者プロフィール◆

国広 洋一（くにひろ・よういち）．東京多摩在住の組み込み系ツール企業勤務エンジニア．『基本から学ぶソフトウェアテスト』の勉強会に参加したことをきっかけに，社外の勉強会にときおり参加しています．TEF（Testing Engineer's Forum；ソフトウェアテスト技術者交流会）やSQiP（Software Quality Profession，スキップと発音する）の勉強会に行くと会えるかも．TestLink日本語化部会のメンバでもあります．オープン・ソースのテスト管理ツールであるTestLinkをどうぞよろしく．