暮らしに役立つQC七つ道具(4) ―― ヒストグラム:「全体」の「傾向」をつかむ
この連載では,ソフトウェア開発の品質管理(QC:Quality Control)において使われている七つの技法「QC七つ道具」について解説している.今回は,分散やバラツキから全体の傾向をつかむのに役立つ「ヒストグラム」を取り上げる.ヒストグラムにより,階級ごとのバラツキが一目で分かるようになる.(編集部)
●七つ道具その4: ヒストグラム
今回取り上げるQC七つ道具は,「ヒストグラム」です.ヒストグラムとは,測定した値を区間(階級)に分けて,データの個数をグラフ化したもので,度数分布図とも呼ばれます.
ヒストグラムは,データの全体的な分布の傾向や偏りを確かめるのに使われ,分布の形や中心の位置,バラツキの大きさなどを見ることによって問題点を明らかにすることができます.
一般的に,製造工程のバラツキは,正規分布注1になるのがよいとされています.
注1:正規分布は,数学の確率論で使われる言葉です.平均値を中心に左右対称な山形で表されるようなデータの分布を指します.学校時代にお世話になった偏差値(学力偏差値)が,正規分布を利用する典型的な例です.また,品質管理関係では,よく3σ(シグマ)という言葉が使われますが,それは確率が正規分布に従うとき,±3σ内に 99.74% の範囲のデータが含まれるからです.この範囲外のデータが検出された場合には何か異常が起こっている可能性が高いので,チェックをする目安になります.このあたりの詳細な説明は私の手に余りますので,詳しくお知りになりたい方は数学の参考書などをお読みください.(^ ^; |
以下,ヒストグラムの例を図1に示します.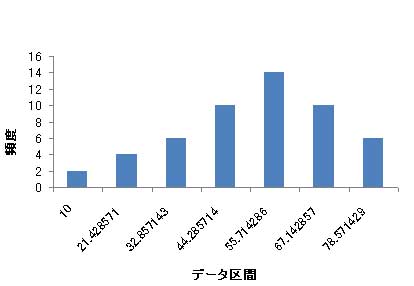
[図1]ヒストグラムの例
単なる棒グラフに見えますが,縦軸が度数分布になるので,横軸の数値の上ではなく,数値の間に棒が書かれるのが特徴です.また,ヒストグラムは,ある程度のデータがないと誤差が大きすぎて意味を持ちません.最低でも50,できれば100以上のデータが必要です.
通常,分析の方法によって,同じデータでも「見える」結果は異なります.今回のヒストグラムと前回紹介したパレート図が,よい例です.パレート図が個別の問題を見つけるために使えるのに対して,ヒストグラムは全体的な問題を見つけるために使えます.
また,データを多面的に分析するということは,複数の「視点」を持つことです.色々な角度から見ることができると,問題を見つけられる可能性が高くなります.さらに,複数の「視点」を持つことは,新たな「視点」を見つけることが容易になるという利点もあるでしょう.


