HDL時代に求められる論理回路設計とは ―― 回路記号を使わない設計手法の考え方

3．論理設計に必要な数学の復習

　論理設計の工程では，小難しい数学的知識をそれほど必要としません．もちろんアルゴリズムを回路で実現するためには，そのアルゴリズムを理解するために微積分や行列演算，さらに三角関数などが必要になるかもしれません．しかし設計工程に移ってからは，これらを直接使うことはありません．

　しかし，まったく数学と縁がなくなってしまったわけではありません．設計だけでなく会話についていくためにも，ここでは最低限必要な数学的知識を紹介します．

●周波数と周期

　図6に示すように，繰り返し波形において，1s（秒）当たりの繰り返しの数が周波数です．論理回路に欠かせない信号にクロックがあり，これは繰り返し波形です．クロックの性質を表す場合に周波数を使います．

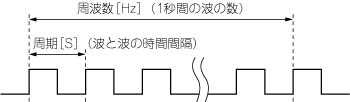
図6　周波数と周期
繰り返し波形において，1s(秒）当たりの繰り返しの数が周波数．周波数の逆数が周期．

　最近のパソコンのCPUのクロックは2GHz～3GHzですが，論理設計では数百MHzが上限です．1GHzを超えられるのは，CPUなどの専用チップだけです．本特集で用いるFPGAは能力的には高いのですが，基板上は10MHzを供給しています．

　周波数の逆数が周期です．周波数をf，周期をTとしたとき，

の関係があります．回路の遅延量を検討する場合に，周期を基準に判断することもあります．設計においてはとても重要な物理量です．電卓などを使わなくても，およその値が分かるようになってください．例えば，周波数が10MHzなら周期は100nsだと即座に答えられるようにしてください．

　そのためには常識的な値の範囲を知っておくとよいでしょう．クロックでしたら，周波数は数MHz～数百MHzですので，周期は数ns～数百nsになります．これ以外の値が出てきたら，よほど特殊か誤っていると思ったほうがいいでしょう．

●補助単位

　周波数と周期の説明で，M（メガ）やn（ナノ）が出てきました．これらを補助単位と呼び，103（もしくは10－3）ごとに用意されています（表1）．M，G（ギガ），T（テラ）など値の大きい方は，パソコンなどでなじみ深いですが，nやp（ピコ）は日常では使いませんのでうろ覚えかもしれません．しかし設計工程では毎日出てきますので，しっかり覚えてください．

表1　補助単位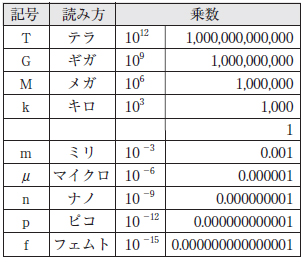

　周波数と周期の一般的な値の範囲では，

もしくは，

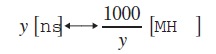
となりますので，Mとnは，1000を割ることで対応していると考えれば変換が容易です．

　例えば，周期が33nsなら1000/33＝30［MHz］のように，割りきれなくてもおよその値を暗算で求められます．

●ブール代数

　論理回路を扱う上では，やはりブール代数は必須です．言語設計ではブール代数を駆使して論理圧縮するようなことはないと説明しましたが，ブール代数そのものを否定したわけではありません．

　回路を論理式で表すことは多いので，AND，OR，NOTの論理演算は必須の概念です．表2に示したブール代数式は，論理設計者にはやはり必須の知識です．

表2　ブール代数

●基数

　論理回路で扱う状態は'1'と'0'だけですから，数値表現としては2進数を用いることになります．ただし多ビットの信号を2進数だけで表すのは煩雑ですので，16進数を使ったり，10進数を使うことがあります．これらの数値表現の相互の変換は，関数電卓などで求めることができますが，表3に示した4ビット程度の数値の範囲は丸暗記してください．

表3　基数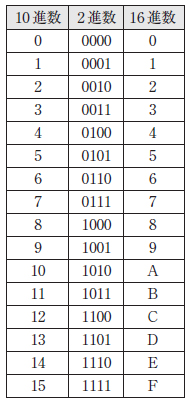

　「2進数で"1101"は，16進数でいくつ？」と聞かれたら，数秒以内に「D」と答えられるようにしておきましょう．

　当たり前のことですが，2進，10進，16進数のいずれで表現しても値は同じです．2進数で表現したものを16進数にしたら数が減った，などということは起こり得ません．表示するけた数は減りますが，数は同じままです．

　本特集では，その時々によって表現の仕方を変えます．理解しやすさに応じて，2進数や10進数で表現しますが，値は同じであることを覚えておいてください．

　なお，N進数のNのことを基数といいます．

●符号付き数値表現

　演算を行う回路を設計する場合，扱う数値にマイナスが含まれるか否かは設計する回路に影響します．マイナスを含む数値を表現する方法には，表4に示すいくつかの方法があります．多くの場合，2の補数表現を使います．

表4　ビットの符号付き数値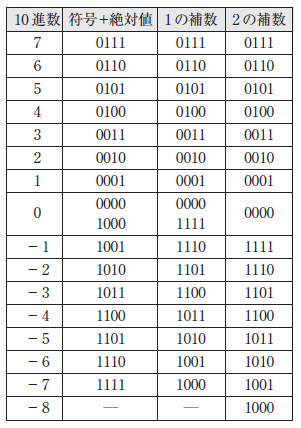

　この表は値が4ビットの場合です．「8ビットなら各値の上位に0を補うだけ」という単純な方法ではありません．また符号付き数値間の演算も，単純に加減算や乗算ができず工夫が必要です．ここでは詳細を省略しますが，符号付き数値を扱う場合には注意が必要だということは覚えておいてください．

参考・引用＊文献
（1） Texas Instruments，Difital Logic Pocket Data Book．
（2） FPGA超入門，ディジタル・デザイン・デクノロジ，No.1，2009年5月．